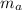 – масса любой порции анилина. Весь анилин, соответственно:
– масса любой порции анилина. Весь анилин, соответственно: 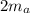
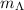 – масса сосуда
– масса сосуда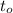 – начальная температура
– начальная температура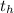 – температура нагретого анилина
– температура нагретого анилина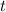 – конечная температура
– конечная температура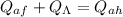 ;
;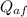 – поглощённое тепло холодного анилина (Aniline Freeze)
– поглощённое тепло холодного анилина (Aniline Freeze) – поглощённое тепло холодного сосуда (Латунь)
– поглощённое тепло холодного сосуда (Латунь)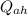 – отдданное тепло горячего анилина (Aniline Hot)
– отдданное тепло горячего анилина (Aniline Hot)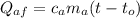 ;
;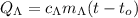 ;
;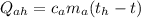 ;
;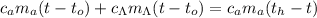 ;
;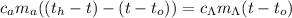 ;
;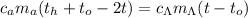 ;
;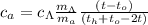 ;
;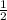 ;
;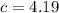 Дж/кгС – теплоёмкость воды
Дж/кгС – теплоёмкость воды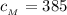 Дж/кгС – теплоёмкость меди
Дж/кгС – теплоёмкость меди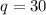 МДж/кг – теплота сгоряния спирта
МДж/кг – теплота сгоряния спирта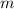 – масса сосуда
– масса сосуда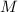 – масса воды
– масса воды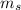 – масса спирта
– масса спирта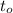 – начальная температура
– начальная температура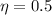 – КПД
– КПД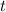 – искомая конечная температура
– искомая конечная температура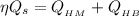 (если вода не закипит, иначе ответ: 100 грудусов), где:
(если вода не закипит, иначе ответ: 100 грудусов), где: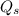 – теплота, выделяемая сжигаемым спиртом
– теплота, выделяемая сжигаемым спиртом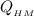 – теплота на нагрев меди
– теплота на нагрев меди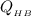 – теплота на нагрев воды
– теплота на нагрев воды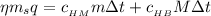 ;
;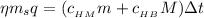 ;
;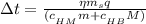 ;
;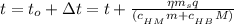 ;
;
Дано:
v = 0,5*V(1-я косм.)
h - ?
Есть формула для центростремительного ускорения:
a = V²/R
Вместо "a" используем ускорение свободного падения:
g = V²/R
Выражая из этой формулы V, получим формулу для первой космической скорости:
V² = gR
V = √(gR), где g - это примерно 9,8 м/с², а R - радиус Земли.
По условию скорость спутника в 2 раза меньше первой космической:
v = 0,5*V(1-я косм.), значит:
v = 0,5*√(gR) - поместим 0,5 под корень:
v = √(0,5²*gR)
C другой стороны есть формула закона всемирного тяготения:
Fтяг = GMm/R², где G - гравитационная постоянная, M - масса Земли, а R - её радиус. Приравняем эту формулу к формуле силы тяжести (т.к. обе, по сути, описывают одно и то же явление, хоть сила тяжести и является частным случаем силы тяготения):
Fтяг = Fтяж
GMm/R² = mg - разделим обе части на "m"
GM/R² = g - это уравнение для "g". Подставим его в выражение для скорости спутника:
v = √(0,5²*gR) = √(0,5²*(GM/R²)R) = √(0,5²*GM/R) - очевидно, что ни к G, ни к M значение 0,5² не может относится, т.к. G - это постоянная, а M - масса Земли, которая вряд ли ни с того ни с сего уменьшилась. Тогда остаётся только радиус. Но земной радиус тоже не может уменьшаться или увеличиваться из-за того, что какой-то спутник летает вокруг Земли. Поэтому вернёмся к формуле для "g":
g = GM/R² - это g, которое у самой поверхности Земли. Чем дальше от поверхности, тем больше становится расстояние, и тем меньше становится g. Получается, что для тел, которые находятся на уже значительном расстоянии от Земли, один лишь радиус использовать нельзя - надо использовать сумму радиуса и высоты:
g = GM/(R + h)² - именно эту формулу мы используем для выражения скорости спутника:
g = v²/(R + h)
v² = g*(R + h)
v = √(g*(R + h)) = √((GM/(R + h)²)*(R + h)) = √(GM/(R + h))
и приравняем её к формуле для половины первой космической скорости, только теперь уже не будем помещать 0,5 под корень:
√(GM/(R + h)) = 0,5√(GM/R) - теперь можно выразить h и найти значение:
√(GM/(R + h)) = 0,5√(GM/R)
√(GM)/√(R + h) = 0,5√(GM)/√R | : √(GM)
1/√(R + h) = 0,5/√R
√(R + h) = 1/(1/(2√R)) | ² - возведём обе части в квадрат
R + h = 4R
h = 4R - R = 3R
Радиус Земли примерно равен 6400 км, тогда:
h = 3R = 3*6400 = 19200 км или 1,92*10^7 м
Проверим:
Масса Земли примерно равна 6*10^(24) кг, тогда:
v = √(GM/(R + h)) = √(6,67*10^(-11)*6*10^(24) / (6,4*10^6 + 1,92*10^7)) = √(6,67*6*10^(13) / (6,4*10^6 + 19,2*10^6)) = √(40,02*10^(13) / (10^6*(6,4 + 19,2))) = √(40,02*10^7/25,6) = 3953,835163 = 3954 м/с
V(1-я косм.) = 0,5√(GM/R) = 0,5*√(6,67*10^(-11)*6*10^(24)/6,4*10^6) = 0,5*√(40,02*10^7/6,4) = 0,5*7907,6703... = 0,5*7908 = 3954 м/с
Всё сходится.
ответ: 19200 км или 1,92*10^7 м.