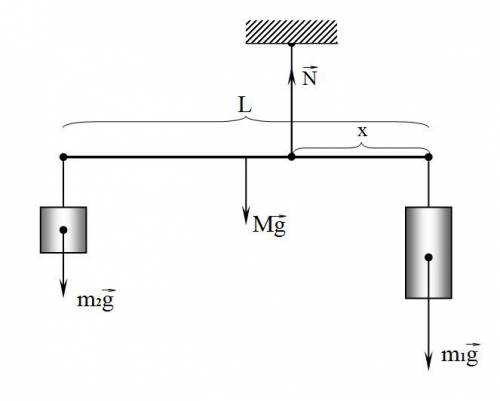
К концам стержня длиной 1 м и массой 5 кг подвешены два груза массами 3 кг и 6 кг. На каком расстоянии от конца стержня с меньшим грузом необходимо закрепить нить, чтобы подвешенный на ней стержень находился в равновесии?
-----------------------------------------
Дано: m = 5 кг; m₁ = 3 кг; m₂ = 6 кг; L = 1 м
Найти: L₂ = L - x ?
--------------------
Обозначим расстояние между точкой подвеса стержня и грузом 6 кг - х. (см. рис.)
Запишем уравнение равновесия:
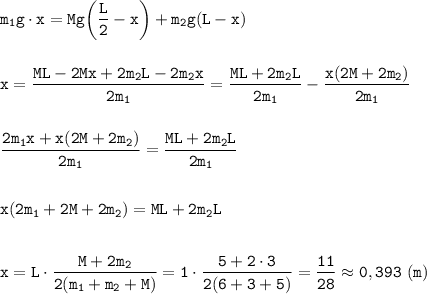
Расстояние от точки подвеса до меньшего груза 3 кг:
L₂ = 1 - 0,393 = 0,607 (м)
1)кратчайший путь - проплыть первпендикулярно
чтобы катер плыл перпендикулярно, он изначально плыл в направлении под углом к перпендикуляру
получается прямоугольный треугольник с гипотинузой u- скорости катера относительно реки , v2 - скорость течения реки
тогда скорость катера отн.берега v^2=u^2-v2^2
v=корень(u^2-v2^2)относительно берега, направление - перпендикулярно берегу
t1=d/v=d/корень(v1^2-v2^2)
2)чтобы время было наименьшим, надо чтобы скорость была наибольшая и путь был наименьшим
v=S/t
S=d/cosa - cosa -косинус ула направления скорости катера к перпендикуляру
v^2=u^2+v2^2-2uvcos(п-п/2+а)=u^2+v2^2+2uvsina
v=корень( u^2+v2^2+2uvsina)
тогда t=d/cosa*( √( u^2+v2^2+2uv2sina))
наибольший косинус и наибольший синус при 45 = √2/2=0.76
t=d/0.76√( u^2+v2^2+1.52uv2) - наименьшее время