Когда растает льдинка в первом сосуде, уровень воды в первом сосуде опустится
Когда растает льдинка во втором сосуде, уровень воды во втором сосуде опустится
Объяснение:
Пусть плотность льда , объем льда , плотность наполнителя полости (воздуха или свинца) , объём полости , плотность воды . Можно считать, что сосуд цилиндрический с площадью сечения S.
Сначала льдинка плавает так, чтобы сила Архимеда компенсировала силу тяжести. Найдём объём погружённой в воду части :
После таяния льда в сосуд добавится вода объёмом
,
а также во втором случае свинца
1) Наполнитель - воздух. Изменение уровня воды:
Плотность воздуха хоть и невелика, но всё же отлична от нуля, значит, высота уменьшится.
2) Наполнитель - свинец. Изменение уровня воды:
Выражение в скобках меньше нуля, значит, и в этом сосуде уровень воды тоже понизится
Когда растает льдинка в первом сосуде, уровень воды в первом сосуде опустится
Когда растает льдинка во втором сосуде, уровень воды во втором сосуде опустится
Объяснение:
Пусть плотность льда  , объем льда
, объем льда 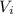 , плотность наполнителя полости (воздуха или свинца)
, плотность наполнителя полости (воздуха или свинца)  , объём полости
, объём полости 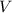 , плотность воды
, плотность воды 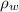 . Можно считать, что сосуд цилиндрический с площадью сечения S.
. Можно считать, что сосуд цилиндрический с площадью сечения S.
Сначала льдинка плавает так, чтобы сила Архимеда компенсировала силу тяжести. Найдём объём погружённой в воду части  :
:
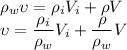
После таяния льда в сосуд добавится вода объёмом
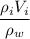 ,
,
а также во втором случае 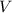 свинца
свинца
1) Наполнитель - воздух. Изменение уровня воды:
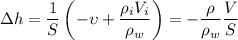
Плотность воздуха хоть и невелика, но всё же отлична от нуля, значит, высота уменьшится.
2) Наполнитель - свинец. Изменение уровня воды:

Выражение в скобках меньше нуля, значит, и в этом сосуде уровень воды тоже понизится
Тх=150 С = (273+150) =423 К
Тн=450 С = (273+450) =723 К
η = (Tн - Тх ) /Тн = 1 - Тх /Тн = 1 -423/723=0.415 (41.5%)
Δη = 15 % ( 0.15)
η1 = η+Δη = 0.415+0.15 = 0,565
η1 = 1 - Тх / Тн1 ;
Тх / Тн1 = 1-η1
Тн1 = Тх / (1-η1) = 423 / (1- 0,565) = 972,4 K = 699,4 C ~~ 700 C
ОТВЕТ 700 С