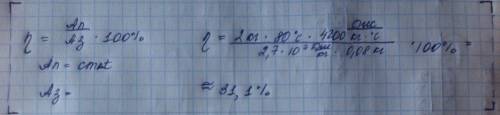
Определите кпд горелки,если при нагревании воды массой 2 кг на 80 ос потребовалось 80 г спирта

👇

Ответ:

huh106

15.03.2021

Решение во вложении, надеюсь, видно
Определите кпд горелки,если при нагревании воды массой 2 кг на 80 ос потребовалось 80 г спирта

4,4(53 оценок)

Открыть все ответы

Ответ:

бооой

15.03.2021

Клевая задача. Максимальная скорость будет в итоге складываться из вертикальной и горизонтальной компонент:
$v= \sqrt{v_y^2+v_x^2}$

Поскольку падение происходит в гравитационном поле, то вертикальная компонента не связана с параметрами капли и зависит только от высоты падения и напряженности поля (ускорения свободного падения), так что с ней все ясно:
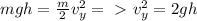
$mgh=\frac{m}{2}v_y^2 =\ \textgreater \ v_y^2=2gh$

Горизонтальная же компонента зависит от силы расталкивания двух частей одной капли. Скорость, приобретенная половинками исходной капли, полностью определит их кинетическую энергию. А по закону сохранения энергии, вся запасенная электростатическая энергия капли разделится между двумя капельками: частично станет их электростатической энергией и частично перейдет в кинетическую (по горизонтальной составляющей скорости). А значит, нам надо найти разность начальной и конечной электростатической энергии. Вот и все.

Начальная энергия капли равна $E_0=4\pi\epsilon_0 R\frac{\phi_0^2}{2}$

После разделения капли на две одинаковые их объемчики будут равны половине объема исходной капли, а отсюда находим их радиусы

:
$\frac{4}{3}\pi R^3=2\cdot \frac{4}{3}\pi r^3$
$r=\frac{R}{ \sqrt[3]{2} }$

Энергия распределится поровну, поэтому суммарная электростатическая энергия двух новых капель составит:
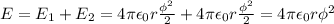
$E=E_1+E_2=4\pi\epsilon_0 r\frac{\phi^2}{2}+4\pi\epsilon_0 r\frac{\phi^2}{2}=4\pi\epsilon_0 r\phi^2$

Потенциал маленькой капли зависит от ее заряда и радиуса. Как изменился радиус мы уже знаем, а вот заряд после разделения распределился пополам - части ведь одинаковые. Поэтому
$\phi=\frac{1}{2}\frac{R}{r}\phi_0= \frac{ \sqrt[3]{2} }{2} \phi_0$

Таким образом, кинетическая энергия, связанная с горизонтальной компонентой скорости, равна
$E_k=\frac{m}{2}v_x^2=E_0-E=4\pi\epsilon_0 R\frac{\phi_0^2}{2}-4\pi\epsilon_0 r\phi^2=4\pi\epsilon_0(R\frac{\phi_0^2}{2}-\frac{R}{ \sqrt[3]{2} }\frac{ (\sqrt[3]{2})^2 }{4}\phi_0^2)$

$E_0-E=4\pi\epsilon_0\phi_0^2R(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})$

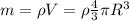$m=\rho V=\rho \frac{4}{3}\pi R^3$ - суммарная масса двух частей, разумеется равна массе исходной капли.

Отсюда
$v_x^2=\frac{2}{\rho \frac{4}{3}\pi R^3}4\pi\epsilon_0\phi_0^2R(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})=\frac{6}{\rho R^2}\epsilon_0\phi_0^2(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})$

$v_x^2=\frac{3\epsilon_0\phi_0^2}{\rho R^2}(1-\frac{\sqrt[3]{2}}{2})$

Окончательно,
$v= \sqrt{v_y^2+v_x^2} = \sqrt{2gh+\frac{3\epsilon_0\phi_0^2}{\rho R^2}(1-\frac{\sqrt[3]{2}}{2})}$

4,6(35 оценок)

Ответ:

anna3371

15.03.2021

Запишем формулу кинетической энергии в малекулярной физике . Нам неизвестна температура, её мы выражаем из уравнения Менделеева-Клайперона ⇒ из данной формулы выражаем температуру ⇒ подставив данную формулу в формулу кинетической энергии

R - универсальная газовая постоянная = 8,31 Дж/моль*К.

k - постоянная Больцмана = 1,38*10⁻²³ Дж/К.

V - объём = 1 м³.

p - давление = 1,5*10⁵ Па.

N - число малекул = 2*10²⁵.

Na - число авагадро = 6*10²³ моль₋₁

Подставляем численные данные и вычисляем ⇒

Джоуль.

ответ: Дж.

4,6(4 оценок)

Это интересно:

Транспорт