 нм имеет энергию
нм имеет энергию 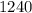 эВ, то фотон с энергией
эВ, то фотон с энергией 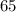 эВ имеет длину волны
эВ имеет длину волны 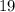 нм, что как раз хорошо бы подошло для этой задачи, поскольку длина волны испущенного фотона должна быть меньше длины поглощённого. А вот если брать без поправки исходное данное в задаче значение
нм, что как раз хорошо бы подошло для этой задачи, поскольку длина волны испущенного фотона должна быть меньше длины поглощённого. А вот если брать без поправки исходное данное в задаче значение 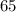 мэВ, т.е. в 1000 раз меньше, то длина волны получится
мэВ, т.е. в 1000 раз меньше, то длина волны получится 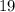 мкм
мкм 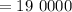 нм, что в
нм, что в 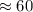 раз больше длины волны падающих фотонов лазера, а значит, энергия поглощалась бы кристаллом, и никакого антистоксового охлаждения бы не наблюдалось. Таким образом, в условии задачи необходимо сделать исправление:
раз больше длины волны падающих фотонов лазера, а значит, энергия поглощалась бы кристаллом, и никакого антистоксового охлаждения бы не наблюдалось. Таким образом, в условии задачи необходимо сделать исправление: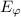 равна НЕ
равна НЕ 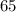 мэВ, а просто –
мэВ, а просто – 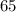 эВ !
эВ !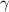 -кванта :
-кванта :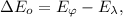 где
где 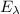 – энергия одного фотона поглощаемых лазерных лучей.
– энергия одного фотона поглощаемых лазерных лучей.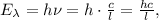 где
где 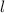 – длина волны лазерных лучей.
– длина волны лазерных лучей.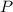 лазерного излучения, попадающего на кристалл, можно вычислить, как
лазерного излучения, попадающего на кристалл, можно вычислить, как 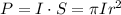 ;
;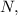 образующих этот поток за время
образующих этот поток за время 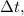 можно найти, как:
можно найти, как: 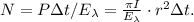
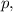 получим, что полное число фотонов
получим, что полное число фотонов 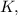 поглощаемых кремнием
поглощаемых кремнием 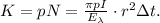
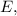 отнятую у нано-кристалла за время
отнятую у нано-кристалла за время 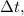 можно найти, перемножив полное число процессов антистоксового пере-испускания, равное числу поглощённых фотонов, на энергию, отнимаемую у вещества в одиночном процессе пере-испускания:
можно найти, перемножив полное число процессов антистоксового пере-испускания, равное числу поглощённых фотонов, на энергию, отнимаемую у вещества в одиночном процессе пере-испускания: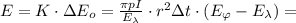
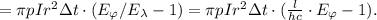
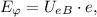 тогда:
тогда: 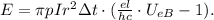
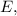 отнятую у нано-кристалла за время
отнятую у нано-кристалла за время 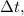 можно найти через:
можно найти через: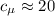 Дж/(K·моль) кремния,
Дж/(K·моль) кремния,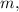 молярную массу
молярную массу 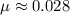 кг/моль,
кг/моль,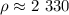 кг/м³ и объём
кг/м³ и объём 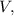 как:
как: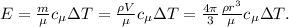
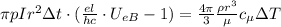 ;
;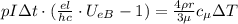 ;
;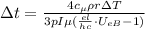 ;
;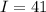 Вт/см²
Вт/см² 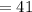 Вт
Вт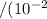 м
м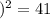 Вт
Вт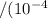 м²
м²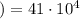 Вт/м² .
Вт/м² .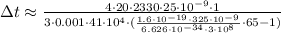 сек
сек 
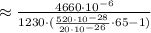 сек
сек 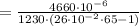 сек
сек 
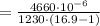 сек
сек 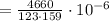 сек
сек 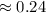 мс .
мс .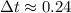 мс
мс
Теперь нам надо записать 2 закон Ньютона в векторном виде: →
→ → → → →
Fтяг+Fтр+mg+N=ma, теперь нам надо найти проекции этих сил на координатные оси ОХ: Fтяг-Fтр - mg sinα=ma (сила трения имеет отрицательную проекцию, тк. она направлена "против" оси ОХ, mg отрицательна т.к. идем от начала проекции к концу против направления оси, а если опустить перпендикуляр из конца вектора на ОХ то получим, что угол 30 будет лежать напротив проекции, т.е сам вектор при этом будет равен mg sinα)
Теперь аналогично находим проекции всех векторов на ОУ: 0+0-mg cosα+N=0 отсюда находим, что N=mg cosα, вспоминаем, что Fтр=μN=μ mg cosα, осталось все собрать в кучу, получаем: Fтяг- μ mg cosα - mg sinα=ma отсюда a=(Fтяг -μ mg cosα -mg sinα)/m=(7000-0,1*1000*10*√3/2 - 1000*10*1/2)/1000=(6150-5000)/1000=1150/1000=1,15 м/с.кв.