ответ: 1.4м/c 1м/c 1м/c 0м/c
Объяснение:
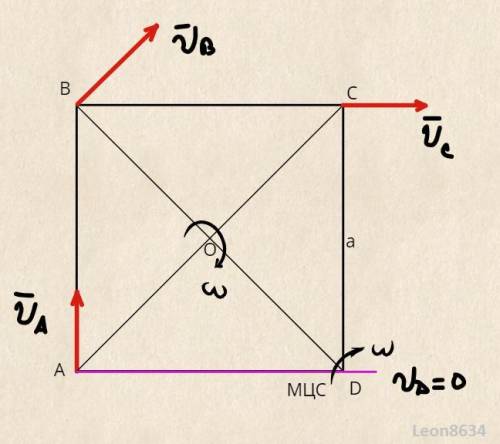
Мгновенный центр вращения квадрата располагается на перпендикуляре к скорости v, а значит лежит на прямой AD. Известно, что угловая скорость вращения ω =4 рад/c. Чтобы найти скорость v, нужно умножить расстояние от центра вращения на угловую скорость вращения. Определим расстояние от центра вращения:
x =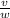 
= 0.25м
Заметим, что это расстояние в точности равно стороне квадрата. Известно, что скорость v направлена к точке В, а также, что направление обхода вершин квадрата совпадает с направлением его вращения. Это значит, что из двух точек лежащих на прямой AD, нам подходит только точка D => точка D является мгновенным центром вращения и ее скорость равна 0.
Теперь легко определяем скорости точек C и B:
Vc = ωa = 1м/c
Vb = ω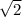
a = 1.4 м/c
Для случая, когда направление вращения совпадает с направлением обхода:
0; 1; 1,41
Для случая, когда направление вращения противоположно направлению обхода:
1,41; 2; 2,24
Объяснение:
Определим положение мгновенного центра скоростей. Очевидно, он лежит на перпендикуляре к скорости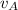 
. Расстояние до него:
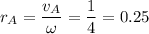м
Значит, мгновенный центр скоростей совпадает с вершиной D квадрата.
Скорости остальных вершин:
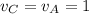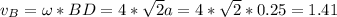м/с
м/с
Для случая вращения против направления обхода вершин задача была решена мной 26.07.2020, значения скоростей прикрепляю в шапку.
Объяснение:
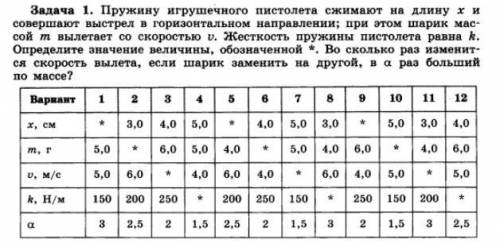
1) x=0.03 м m=0.004 кг k=200 Н/м α=3 v=? v/v2=?
===
m*v²/2=k*x²/2
v=x*√(k/m)=0.03*√(200/0.004)≈6.7 м/с
v2=0.03*√(200/(3*0.004))≈3.87 м/с
v/v2=6.7/3.87=1.73
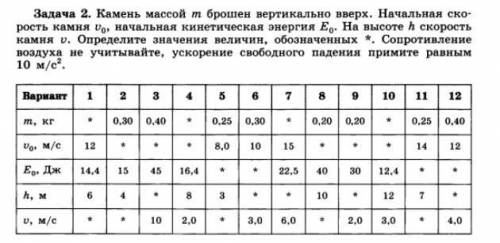
2) m=0.25 кг vo=14 м/с h=7 м Eo=? v=?
===
Eo=m*vo²/2=0.25*14²/2=24.5 Дж
Eo=m*v²/2+m*g*h
v=√(2*(Eo/m-g*h))=√(2*(24.5/0.25-10*7)≈7.48 м/с
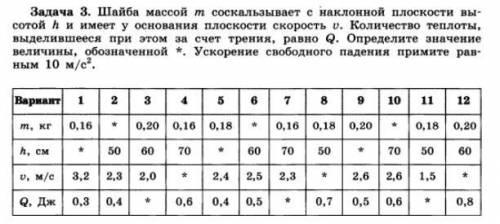
3) m=0.18 кг h=0.5 м v=1.5 м/с Q=?
===
m*g*h=m*v²/2+Q
Q=m*(g*h-v²/2)=0.18*(10*0.5-1.5²/2)≈0.7 Дж