Направим ось ох вдоль поверхности стола. на доску m1 действуют: сила тяжести f1, сила трения fтр со стороны бруска и искомая сила f (для простоты полагаем что она параллельна поверхности) . на брусок m2 действуют: сила тяжести f2 и сила трения fтр. сила трения бруска о доску равна f=nn, где n коэффициент трения, n прижимающая сила. n найдем из уравнения движения бруска по оси оу (не движется. т. е. а (у) =0). m2a(y)=m2g-n=0, отсюда n=m2g и сила трения fтр=nm2g. трение доски о поверхность отсутствует. запишем уравнения движения доски и бруска по оси ох. (m1+m2)*a(x)=f-fтр=f-nm2g (1) m2*a(x)=fтр=nm2g (2). из (2) a(x)=ng и из (1) f=(m1+m2)*ng+nm2g=ng(m1+2m2).
Масса автомобиля:
т = 
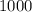кг.
Начальная скорость автомобиля: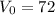
км/ч = 
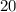м/с.
Конечная скорость автомобиля: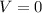
м/с.
Так как автомобиль остановится.
Коэффициент трения:
.
Найти нужно тормозной путь: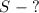
Решение:0. Строим рисунок для упрощения определения направлений сил.
1. Распишем второй закон Ньютона по оси Оy: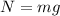
.
2. Распишем второй закон Ньютона по оси Ох:
.
3. Сила трения по определению:
4. Объединим (1) и (3):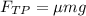
.
5. Объединим (2) и (4):
.
6. Скорость при равнозамедленном движении: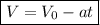
С учётом того, что конечная скорость равна нулю, получим: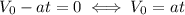
.
7. Объединяем (5) и (6):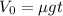
.
8. Выразим время из (7):
.
9. Тормозной путь: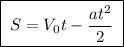
10. Объединяем (5), (8) и (9):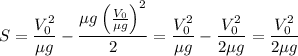
.
Численно получи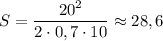м:
(м).
ответ: 28,6 м.Более простой по закону сохранения энергии.