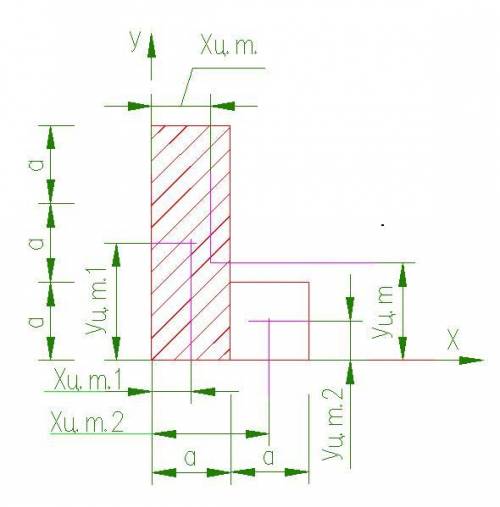
Объяснение:
Пластина делится на две прямоугольные части.
У прямоугольника центр тяжести в середине.
У первой - заштрихованной пластины площадь 3a^2
А расстояния от координатных осей до центра тяжести:
Хцт1=0,5а
Уцт1=1,5а
У второй пластины площадь a^2
расстояния от координатных осей до центра тяжести:
Хцт2=1,5а
Уцт1=0,5а
Центр тяжести можно найти если просуммировать площади умноженные на расстояние до центра тяжести каждой простой фигуры, а потом эту сумму поделить на общую площадь.
Общая площадь фигуры 4а^2
Остается посчитать
Хц.т.=(3a^2*0,5а+a^2*1,5а)/4а^2=3а^3/4а^2=3а/4=0,75а
Уц.т.=(3a^2*1,5а+a^2*0,5а)/4а^2=3а^3/4а^2=5а/4=1,25а
Картинка приложена
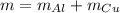
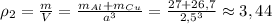 [г/см³]
[г/см³]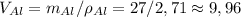 [см³]
[см³] [см³]
[см³]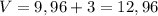 [см³]
[см³]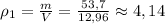 [г/см³]
[г/см³]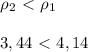
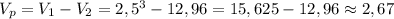 [см³]
[см³]
Определите показания вольтметра в цепи, изображенной на рис., если E = 15 В, R1 = 2 Ом, R2 = 4 Ом, R3 = 6 Ом, R4 = 12 Ом, R5 = 2 Ом.