Длина: 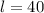 см =
см = 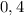 м.
м.
Высота: 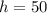 см =
см = 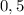 м.
м.
Ширина: 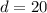 см =
см = 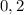 м.
м.
Масса канистры: 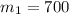 г =
г = 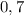 кг.
кг.
Найти нужно общий вес бензина и канистры: 
1. Найдём объём канистры: 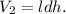
2. Используя объём канистры, предполагая, что бензин занимает его полностью, и найдя плотность бензина в таблице плотностей: 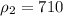 кг/м³, можем найти массу бензина:
кг/м³, можем найти массу бензина: 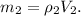
3. Общая масса бензина с канистрой: 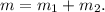
4. Вес, в данной задаче равный силе тяжести, находим по формуле: 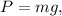 где
где 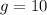 м/с² - ускорение свободного падения.
м/с² - ускорение свободного падения.
5. Объединяем всё вышенаписанное в одну формулу: 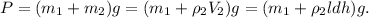
Численно получим:
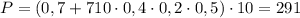 (Н).
(Н).
Жёсткость пружины: 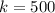 Н/м.
Н/м.
Удлинение пружины: 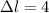 см =
см = 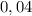 м.
м.
Найти нужно массу груза: 
0. Сделаем небольшой рисунок, чтобы увидеть, как и какие силы действуют на груз.
1. Распишем второй закон Ньютона для данного рисунка: 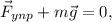 где
где 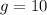 м/с² - ускорение свободного падения.
м/с² - ускорение свободного падения.
2. В проекции на ось Оу (1) перепишется так: 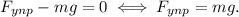
3. Вспоминаем классическую формулу для силы упругости: 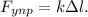
4. Объединяем (2) и (3): 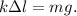
5. Выразим массу из (4): 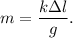
Численно получим:
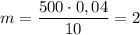 (кг).
(кг).
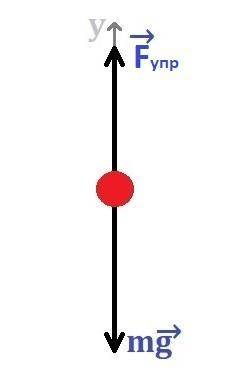
Тело, которое соскальзывает вниз по наклонной плоскости. В этом случае на него действуют следующие силы:
Сила тяжести mg, направленная вертикально вниз;
Сила реакции опоры N, направленная перпендикулярно плоскости;
Сила трения скольжения Fтр, направлена противоположно скорости (вверх вдоль наклонной плоскости при соскальзывании тела).
Введем наклонную систему координат, ось OX которой направлена вдоль плоскости вниз. Это удобно, потому что в этом случае придется раскладывать на компоненты только один вектор — вектор силы тяжести mg, а вектора силы трения Fтр и силы реакции опоры N уже направлены вдоль осей. При таком разложении x-компонента силы тяжести равна mg sin(α) и соответствует «тянущей силе», ответственной за ускоренное движение вниз, а y-компонента — mg cos(α) = N уравновешивает силу реакции опоры, поскольку вдоль оси OY движение тела отсутствует.
Сила трения скольжения Fтр = µN пропорциональна силе реакции опоры. Это позволяет получить следующее выражение для силы трения: Fтр = µmg cos(α). Эта сила противонаправлена «тянущей» компоненте силы тяжести. Поэтому для тела, соскальзывающего вниз, получаем выражения суммарной равнодействующей силы и ускорения:
Fx = mg( sin(α) – µ cos(α) );
ax = g( sin(α) – µ cos(α) ).
ускорение:
аx= v/t
скорость равна
v=ax*t=t*g( sin(α) – µ cos(α) )
через t=0.2 с
скорость равна
v=0.2*9.8(sin(45)-0.4*cos(45))=0.83 м/с
Дано:
V=0, 01 м³
р=800 кг/м³
Знайти: Fв-?
Fв=рgV=800×10×0,01=80 H.
В-дь: Fв=80 Н