 м ;
м ;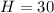 м .
м . ;
; .
.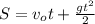 :
: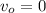 , а значит:
, а значит:  ;
; , откуда:
, откуда: 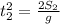 ;
;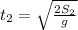 ;
;![t_2 = \sqrt{ \frac{ 2 * 2 [ {}_M ] }{ 9.8 [ {}_M/c^2 ] } } = 0.64 c](/tpl/images/0478/7687/31fb6.png) .
.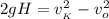 :
: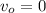 , а значит:
, а значит: 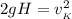 ;
;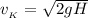 ;
;![v_{_K} = \sqrt{ 2 * 9.8 [ {}_M/c^2 ] * 30 [ {}_M ] } = 24](/tpl/images/0478/7687/9f655.png) м/с ;
м/с ;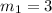 кг ;
кг ; ;
;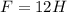 ;
;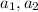 .
.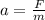 ;
;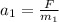 ;
; ;
;![a_1 = \frac{12H}{ 3 [ {}_{ K \Gamma } ] } = 4](/tpl/images/0478/7687/b6139.png) м/с² ;
м/с² ; м/с²
м/с²  м/с² ;
м/с² ; м/c ;
м/c ; .
.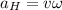 , где
, где 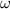 – угловая скорость часовой стрелки.
– угловая скорость часовой стрелки.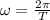 , где T – период вращения часовой стрелки.
, где T – период вращения часовой стрелки.
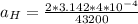 м/с²
м/с² 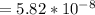 м/с²
м/с² 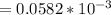 мм/с²
мм/с² 
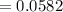 мкм/с²
мкм/с²  нм/с² ;
нм/с² ; м ;
м ;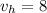 м/с .
м/с .
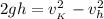 :
: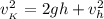 ;
;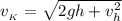 ;
;![v_{_K} = \sqrt{ 2gh + v_h^2 } = \sqrt{ 2 * 9.8 [ {}_M/c^2 ] * 2.9 [ {}_M ] + 8^2 [ {}_{M^2} / {}_{c^2} ] } =](/tpl/images/0478/7687/aa6ad.png)
![= \sqrt{ 121 [ {}_{M^2} / {}_{c^2} ] } = 11](/tpl/images/0478/7687/f565f.png) м/с ;
м/с ;
• дабы облегчить дальнейшие расчеты, сразу вычислим значение косинуса угла наклона плоскости к горизонтали:
○ cosα = √(1-0.1²) ≈ 0.994
• напишем уравнения динамики в проекции на ось, направленную вдоль плоскости и сонаправленную с ускорением автомобиля и прицепа (к слову, они равны, так как допускаем, что трос нерастяжимый; силы натяжения равны по 3 закону Ньютона)
○ Fтр - T - m1gsinα = m1a
○ T - m2gsinα = m2a
• сила трения равна по закону Кулона-Амонтона Fтр = u N = u m1gcosα. учитывая это, складываем уравнения:
○ m1g (u cosα - sinα) - m2gsinα = a (m1 + m2)
○ a = (g (m1 (u cosα - sinα) - m2sinα))/(m1 + m2)
• чтобы не допустить в дальнейшем вычислительной ошибки, посчитаем ускорение отдельно:
○ a ≈ 0.6 м/c²
• из уравнения динамики для прицепа получаем:
○ T = m2 (g sinα + a) = 1600 H