• От города до оазиса: 30 км. со скоростью 15 км/ч ⇒ 30 / 15 = 2 часа в пути.
• Время отдыха, то есть 1/2 пути от города до оазиса: 2 (часа) /2 = 1 (час)
• От оазиса до города: 30 км. со скоростью 10 км/ч ⇒ 30 / 10 = 3 часа в пути.
Следовательно, кавалерист отсутствовал в городе 6 часов (2 + 1 + 3)
Средняя путевая скорость (был в пути 2 + 3 = 5 часов): 60 / 5 = 12 (км/ч)
ответы:
1) Отсутствовал в городе: 6 часов
2) Средняя путевая скорость: 12 км/ч
При движении по окружности возникает центростремительное ускорение, которое находится по формуле:
a = v²/R. Здесь v - линейная скорость вращения точки, а R - радиус окружности, который кстати сказать мы не знаем. Найдём его.
Линейная скорость вычисляется по формуле
v = ωR - где ω - угловая скорость вращения точки, а R - как раз нужный нам радиус.
Найдём теперь угловую скорость вращения. Это отношение угла поворота ко времени, за которое этот угол был пройден:
Точка по условию 1/6 * 2π = π/3 радиан.
Отсюда угловая скорость вращения:
ω = π/3 : 1 = π/3 радисан в секунду.
теперь мы знаем линейную и угловую скорость вращения, найдём отсюда радиус окружности:
R = v / ω = 10 / π/3 = 30/π = 10 м - это приблизительно.
Отсюда найдём ускорение:
a = 10 м/c²
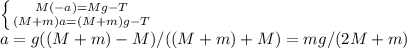
1)6часов
2)10км/ч
Объяснение:
15×2=30
и стоит он ровно один час
потом едет со скоростью 10км/ч расстояние 30км
t3=3 часа
t1=2 часа
t2=1 час когда он стоял и отдыхал
средняя скорость равна S(total)/(t total)
Расстояние полное равен 2S потому что он пошел и пришел обратно, и с временем тоже самое 6 часов
30×2/6=10