Объяснение:
Дано:
ε₁ = 14 В
ε₂ = 14 B
R₁ = 1 Ом
R₂ = 2 Ом
R₃ = 2 Ом
__________
U₂ - ?
I₂ - ?
Составить уравнения Кирхгофа.
I₁ - ?
I₃ - ?
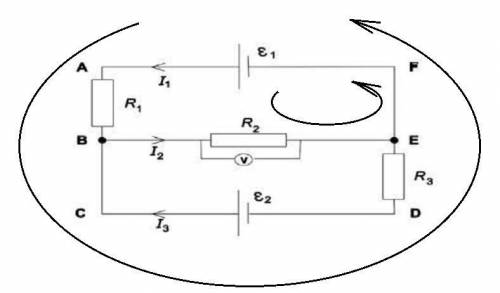
а)
Определите по рисунку показание вольтметра:
U₂ = 12 B.
Сила тока: через резистор R₂:
I₂ = U₂ / R₂ = 12 / 2 = 6 A (1)
c)
Напишем уравнение для цепи, представленной на рисунке, применив первое правило Кирхгофа (для узла В):
I₁ - I₂ + I₃ = 0
С учетом (1):
I₁ + I₃ = 6 A (2)
d)
Напишем уравнение, применив второе правило Кирхгофа для контура ABEFA:
I₁R₁ + I₂R₂ = ε₁
1·I₁ + 6·2 = 14
I₁ = 2 А
Тогда, с учетом (2)
I₃ = I₂ - I₁ = 6 - 2 = 4 А
Напишем уравнение, применив второе правило Кирхгофа для контура ABCDEFA:
I₁R₁ - I₃R₃ = ε₁ - ε₃
Человек, рост которого составляет h = 189 см, стоит под фонарём. Его тень при этом составляет L° = 170 см. Если он отойдёт от фонаря ещё на x = 0,18 м = 18 см, то его тень станет равна L” = 206 см. На какой высоте над землёй висит фонарь?
Чёрный треугольник: Н/h = AD/L° = AD/170; (*)
Красный треугольник: Н/h = AC/L” = AC/206. (**)
Но DС = L”+ x – L° = 206 + 18 – 170 = 54 см. (***)
Делим (**) на (*): 1 = (АС/206)/(AD/170), откуда: (АС/206) = (AD/170) или:
АС = 1,21*AD.
Но из (***): DC = 54 см. Или AC – AD = 54. ==> 1,21*AD – AD = 54 ==> 0,21*AD = 54 ==> AD = 257,1 см.
Подставив AD в (*), получим: 170*H = h*AD ==> H = h*257,1/170 = 189*257,1/170 = 285.8 см.
Итак, фонарь висит на высоте Н = 286 см.
900*3=2700