ответ:решай по этой задаче
Человек, рост которого составляет 179 см, стоит под фонарём. Его тень при этом составляет 161 см. Если он отойдёт от фонаря ещё на 0,1 м, то его тень станет равна 181 см. На какой высоте над землёй висит фонарь?
Объяснение:
Дано: H = 179, S1 = 161, S2 = 181
Обозначим: Y - высота фонаря, X1, X2 = X1 + 10 - расстояния до фонаря (все меряем в сантиметрах). Тогда из подобия треугольников
Y/H = (X1+S1)/S1 = (X2+S2)/S2 = (X1+10+S2)/S2.
Решаем эту систему относительно X1,Y (потом X1 выбрасываем). Для Y получаем формулу
Y = H * (S2 - S1 + 10) / (S2 - S1) = 179*30/20 = 268.5
Округляем до точности исходных данных.
ответ: 2 м 69 см
ответ:решай по этой задаче
Человек, рост которого составляет 179 см, стоит под фонарём. Его тень при этом составляет 161 см. Если он отойдёт от фонаря ещё на 0,1 м, то его тень станет равна 181 см. На какой высоте над землёй висит фонарь?
Объяснение:
Дано: H = 179, S1 = 161, S2 = 181
Обозначим: Y - высота фонаря, X1, X2 = X1 + 10 - расстояния до фонаря (все меряем в сантиметрах). Тогда из подобия треугольников
Y/H = (X1+S1)/S1 = (X2+S2)/S2 = (X1+10+S2)/S2.
Решаем эту систему относительно X1,Y (потом X1 выбрасываем). Для Y получаем формулу
Y = H * (S2 - S1 + 10) / (S2 - S1) = 179*30/20 = 268.5
Округляем до точности исходных данных.
ответ: 2 м 69 см
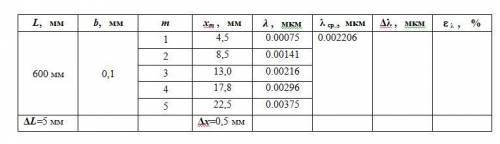
Лабораторная работа № 6
«Измерение длины световой волны»
Оборудование:
1. Дифракционная решетка с периодом 1/100 мм.
2. Измерительная установка.
Подготовка к работе:
1) Подготовим бланк отчета.
2) Собираем измерительную установку, установив экран на расстоянии 40 см от решетки.
3) Снимаем показания.
Для расчетов используем формулу:
λ = d*b / (k*a)
где d – период дифракционной решетки;
b – расстояние до центра спектральной линии;
a – расстояние от решетки до экрана;
k – порядок спектра.
Получили (см. таблицу измерений)
Посмотрим на иллюстрацию (см. вкладку)
Вывод: мы достаточно точно рассчитали длины волн.
Объяснение:
привет