Температура повітря по всій висоті шахти стала і дорівнює t =23 С. Глибина шахти h = 3км. Тиск повітря на поверхні Землі р0 =755 мм .рт. ст. Яка густина повітря на дні шахти
1. Введем прямоуголную систему координат следующим образом, полож. нарпавление оси Оу совпадает с направлением начальной скорости тела, а полож. направление оси Ох совпадает с направлением скорости тела через 5 с, то есть перпендикулярно (по усл.)
2. В векторном виде: S(суммарное)=S(по оси Ох)+S(по оси Оу).
Т.к. угол между векторами 90, то S(суммарное) найдем по теореме Пифагора, зная перемещение вдоль оси Ох, и перемещение вдоль оси Оу.
3. Пусть v0 - начальная скорость, v - скорость тела через время t=5с, y - перемещение тела вдоль оси Оу, х - перемещение тела вдоль оси Ох, угол а - угол между вектором v0 и горизонтом, (а также угол между вектором g и осью Ох), тогда:
Oy: 0=v0-g*sin a*t, где t = 5 c, то есть v0=g*sin a*t
Ox: v=0+g* cos a*t, то есть v=g*cos a*t
y=v0*t - ; так как v0=g*sin a*t, то:
y =
x=
4. s=√
s=√, согласно основному тригонометрическому тождеству выражение под корнем равно 1, следовательно корень равен 1, а значит:
Q1=Q2+Q3+Q4 где Q1 - количество теплоты отнятое у воды и льда Q2 =сm(t1-t2) - количество теплоты отданное водой для того чтобы понизить свою температуру до 0 градусов. t1=20 град, t2= 0 град. с=4200, m=200 гр = 0,2 кг Q3 =km- количество теплоты, отданное водой, чтобы криссталлизоваться в лед. k = 2100 - удельная теплота плавления (криссталлизации) воды Q4 = cm(t2-t3) t3= - 5 град. , m= 0 ,2 кг - количество теплоты, отданное льдом, чтобы понизить свою температуру до - 5 град Подставляем и находим, то что нам нужно, т. е. Q1
Задача №7
1. Введем прямоуголную систему координат следующим образом, полож. нарпавление оси Оу совпадает с направлением начальной скорости тела, а полож. направление оси Ох совпадает с направлением скорости тела через 5 с, то есть перпендикулярно (по усл.)
2. В векторном виде: S(суммарное)=S(по оси Ох)+S(по оси Оу).
Т.к. угол между векторами 90, то S(суммарное) найдем по теореме Пифагора, зная перемещение вдоль оси Ох, и перемещение вдоль оси Оу.
3. Пусть v0 - начальная скорость, v - скорость тела через время t=5с, y - перемещение тела вдоль оси Оу, х - перемещение тела вдоль оси Ох, угол а - угол между вектором v0 и горизонтом, (а также угол между вектором g и осью Ох), тогда:
Oy: 0=v0-g*sin a*t, где t = 5 c, то есть v0=g*sin a*t
Ox: v=0+g* cos a*t, то есть v=g*cos a*t
y=v0*t -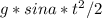
; так как v0=g*sin a*t, то:
y =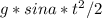
x=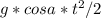
4. s=√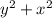
s=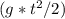
√
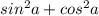, согласно основному тригонометрическому тождеству выражение под корнем равно 1, следовательно корень равен 1, а значит:
s=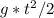
s=10*4*4/2=80(м)
ответ: 80 м