В этой теме рассматривается случай, когда силы действуют вдоль оси бруса (осевое растяжение и сжатие). Изучение необходимо начинать с выяснения во о внутренних силовых факторах, действующих в сечениях стержня.
Применение метода сечений позволяет найти величину и направление равнодействующей внутренней (продольной) силы упругости в рассматриваемом сечении. Следует иметь в виду, что в поперечном сечении, перпендикулярном оси стержня, возникают только нормальные напряжения, которые, в силу гипотезы плоских сечений, равномерно распределены в плоскости сечения и определяются по формуле:
,
где N - внутренняя сила, A - площадь поперечного сечения.
Необходимо знать обе формы записи закона Гука, усвоить такие понятия, как модуль упругости при растяжении- сжатии, коэффициент Пуассона. Ознакомиться с методикой испытаний на растяжение, обработки диаграммы растяжения образца из малоуглеродистой стали с её характерными участками. При экспериментальном изучении растяжения и сжатия необходимо усвоить во определения характеристик прочности материала; пределов пропорциональности, упругости, текучести и прочности (временное сопротивление), учесть, что численные их значения условны, так как для их нахождения соответствующие силы делят на первоначальную площадь поперечного сечения испытываемого образца.
Объяснение:
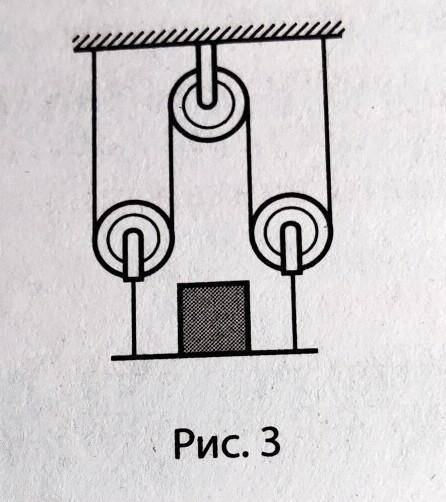
Позначимо літерою а мотузку, перекинуту через блоки, літерами Ь та с мотузки, до
яких прикріплена підставка вантажу. Сили натягу мотузок b та с рівні: Fh= Fc- F.
Вага вантажу дорівнює сумі сил натягу мотузок b та с: P = Fb+Fc -2F. Тоді
F = P/2-mg/2 Отже, сили натягу мотузок b та с: Fb = Fc =mg/2.
Рухомий блок, до обойми якого прикріплено мотузку Ь, дає виграш у силі в 2 ра-
зи, отже, сила натягу мотузки а становить: Fa F/2 = mg/4