5. Баскетбольный мяч, массой 0.6 кг, проходя баскетбольное кольцо, падает на землю и в момент падения имеет скорость 8 м/с. Сопротивлением воздуха пренебречь. Принять g=10 Н/кг.
а) Чему равна кинетическая энергия баскетбольного мяча в момент падения.
[2]
b) Запишите закон сохранения механической энергии для мяча.
[1]
с) Определите на какой высоте находится баскетбольное кольцо, если считать, что в момент
прохождения кольца скорость баскетбольного мяча равна нулю (v = 0).
[2]
d) Определите потенциальную энергию деформированного мяча, если в момент падения на землю
баскетбольный мяч деформировался на 0,02 м. Жёсткость резины принять равной k = 96-10 Н/м.
[2]
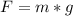 , где g примерно равно 10. То есть сила, которую ты оказываешь стоя на месте равна 530 ньютонов. Теперь, зная площадь и силу, мы можем найти давление, просто подставив значения в формулу
, где g примерно равно 10. То есть сила, которую ты оказываешь стоя на месте равна 530 ньютонов. Теперь, зная площадь и силу, мы можем найти давление, просто подставив значения в формулу 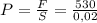 .(Здесь я взял площадь твоего ботинка равной 200 квадратных сантиметров, просто для удобства). НО надо учесть, что ты стоишь на двух ногах, то есть площадь поверхности тебя и земли составляет 2 ботинка
.(Здесь я взял площадь твоего ботинка равной 200 квадратных сантиметров, просто для удобства). НО надо учесть, что ты стоишь на двух ногах, то есть площадь поверхности тебя и земли составляет 2 ботинка 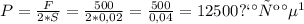 а то есть
а то есть 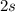 . То есть
. То есть 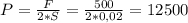 паскалей.Теперь, как я понял, если ты идёшь, то ты отрываешь ногу от земли, то есть ты стоишь некоторое время на одной ноге, то есть площадь соприкосновения тебя и земли составит 1 ботинок, то есть
паскалей.Теперь, как я понял, если ты идёшь, то ты отрываешь ногу от земли, то есть ты стоишь некоторое время на одной ноге, то есть площадь соприкосновения тебя и земли составит 1 ботинок, то есть  . Подставим всё в нашу формулу для давления
. Подставим всё в нашу формулу для давления 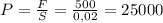 паскалейответ: 1) 12500 паскалей. 2)25000 паскалей
паскалейответ: 1) 12500 паскалей. 2)25000 паскалей
k
m
, где m - масса груза (кг), k - жёсткость пружины (Н/м). Отсюда выражаем искомую массу (чисто математические действия):
\begin{lgathered}T=2\pi\sqrt{\frac{m}{k}} \\(T)^2=(2\pi\sqrt{\frac{m}{k}})^2 \\ T^2=2^2\pi^2*\frac{m}{k} \\T^2=\frac{4*\pi^2*m}{k} \\T^2*k=4*\pi^2*m \\m=\frac{T^2*k}{4*\pi^2}\end{lgathered}
T=2π
k
m
(T)
2
=(2π
k
m
)
2
T
2
=2
2
π
2
∗
k
m
T
2
=
k
4∗π
2
∗m
T
2
∗k=4∗π
2
∗m
m=
4∗π
2
T
По формуле колебаний пружинного маятника T=2\pi\sqrt{\frac{m}{k}}T=2πkm , где m - масса груза (кг), k - жёсткость пружины (Н/м). Отсюда выражаем искомую массу (чисто математические действия):
\begin{lgathered}T=2\pi\sqrt{\frac{m}{k}} \\(T)^2=(2\pi\sqrt{\frac{m}{k}})^2 \\ T^2=2^2\pi^2*\frac{m}{k} \\T^2=\frac{4*\pi^2*m}{k} \\T^2*k=4*\pi^2*m \\m=\frac{T^2*k}{4*\pi^2}\end{lgathered}T=2πkm(T)2=(2πkm)2T2=22π2∗kmT2=k4∗π2∗mT2∗k=4∗π2∗mm=4∗π2T2∗k