
1. Дано:
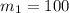 кг
кг
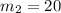 г
г 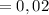 кг
кг
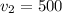 м/с
м/с
Найти: 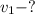
Решение. Имеем замкнутую систему тел, то есть такую систему тел, на которую не действуют внешние силы, а любые изменения состояния этой системы являются результатом действия внутренних сил системы. Значит, можем применить закон сохранения импульса. Поскольку лодка остановится только после трех ударов, то:
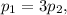
где 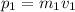 — импульс лодки с охотником,
— импульс лодки с охотником, 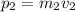 — импульс заряда оружия.
— импульс заряда оружия.
Имеем: 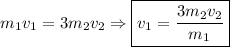
Определим значение искомой величины:
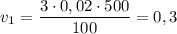 м/с
м/с
ответ: 0,3 м/с.
2. Дано:
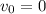
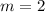 кг
кг
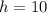 м
м
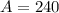 Дж
Дж
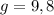 м/с²
м/с²
Найти: 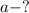
Решение. Совершенная работа состоит из потенциальной и кинетической энергий:
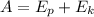
Потенциальная энергия 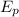 — энергия, которой обладает тело вследствие взаимодействия с другими телами или вследствие взаимодействия частей тела. Потенциальную энергию тела, поднятого над Землей можно найти по формуле:
— энергия, которой обладает тело вследствие взаимодействия с другими телами или вследствие взаимодействия частей тела. Потенциальную энергию тела, поднятого над Землей можно найти по формуле:
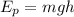
Кинетическая энергия 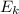 — физическая величина, которая характеризует механическое состояние движущегося тела и равна половине произведения массы
— физическая величина, которая характеризует механическое состояние движущегося тела и равна половине произведения массы 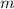 тела на квадрат скорости
тела на квадрат скорости  его движения:
его движения:
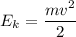
Имеем: 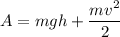
Выразим величину 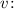
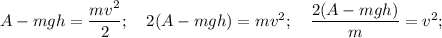
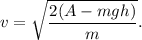
Поскольку тело движется равноускоренно, то имеют место следующие формулы перемещения:
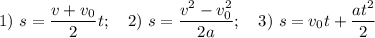
Для данной задачи подойдет формула (2). Здесь 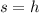 и
и 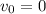
Имеем: 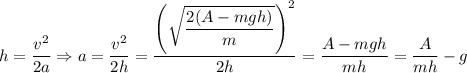
Таким образом, 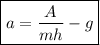
Определим значение искомой величины:
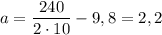 м/с²
м/с²
ответ: 2,2 м/с².
3. Дано:
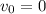
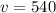 км/ч
км/ч 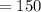 м/с.
м/с.
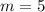 т
т 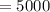 кг
кг
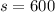 м
м
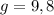 м/с²
м/с²
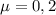
Найти: 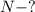
Решение. На самолет действуют четыре силы: сила тяжести 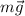 , сила
, сила 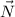 нормальной реакции опоры, сила тяги
нормальной реакции опоры, сила тяги 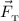 и сила трения
и сила трения 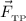
Самолет увеличивает скорость своего движения, значит, ускорение и движение самолета имеют одинаковое направление.
Запишем второй закон Ньютона в общем виде:
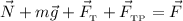
Здесь 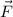 — равнодействующая всех сил.
— равнодействующая всех сил.
Спроектируем уравнение на оси координат:
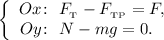
Решим полученную систему, зная что 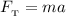 и
и 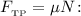
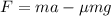
Поскольку самолет движется равноускоренно, то 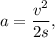 поэтому:
поэтому:
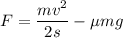
Мощность 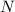 — физическая величина, характеризующая скорость выполнения работы и равная отношению работы
— физическая величина, характеризующая скорость выполнения работы и равная отношению работы 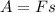 к интервалу времени
к интервалу времени 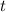 , за который эта работа выполнена:
, за который эта работа выполнена:
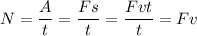
Таким образом, 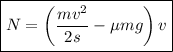
Определим значение искомой величины:
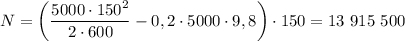 Вт
Вт
ответ: 13,92 МВт.
осмотрим, как влияет э.д.с. самоиндукции на процесс установления тока в цепи, содержащей индуктивность.
в цепи, представленной на схеме 10.10, течёт ток. отключим источник e, разомкнув в момент времени t = 0 ключ к. ток в катушке начинает убывать, но при этом возникает э.д.с. самоиндукции, поддерживающая убывающий ток.
рис. 10.10.
запишем для новой схемы 10.10.b уравнение правила напряжений кирхгофа:
.
разделяем переменные и интегрируем:
пропотенцировав последнее уравнение, получим:
.
постоянную интегрирования найдём, воспользовавшись начальным условием: в момент отключения источника t = 0, ток в катушке i(0) = i0.
отсюда следует, что c = i0 и поэтому закон изменения тока в цепи приобретает вид:
. (10.7)
график этой зависимости на рис. 10.11. оказывается, ток в цепи, после выключения источника, будет убывать по экспоненциальному закону и станет равным нулю только спустя t = ¥.
рис. 10.11.
вы и сами теперь легко покажете, что при включении источника (после замыкания ключа к) ток будет нарастать тоже по экспоненциальному закону, асимптотически приближаясь к значению i0 (см. рис. 10.
. (10.8)
но вернёмся к первоначальной размыкания цепи.
мы отключили в цепи источник питания (разомкнули ключ к), но ток — теперь в цепи 10.8.b — продолжает течь. где черпается энергия, обеспечивающая бесконечное течение этого убывающего тока?
ток поддерживается электродвижущей силой самоиндукции e = . за время dt убывающий ток совершит работу:
da = eси×i×dt = –lidi.
ток будет убывать от начального значения i0 до нуля. проинтегрировав последнее выражение в этих пределах, получим полную работу убывающего тока:
. (10.9)
совершение этой работы сопровождается двумя процессами: исчезновением тока в цепи и исчезновением магнитного поля катушки индуктивности.
с чем же связана была выделившаяся энергия? где она была локализована? располагалась ли она в проводниках и связана ли она с направленным движением носителей заряда? или она локализована в объёме соленоида, в его магнитном поле?
опыт даёт ответ на эти вопросы: энергия электрического тока связана с его магнитным полем и распределена в пространстве, занятом этим полем.
несколько изменим выражение (10.9), учтя, что для длинного соленоида справедливы следующие утверждения:
l = m0n2sl (10.5) — индуктивность;
b0 = m0ni0 (9.17) — поле соленоида.
эти выражения используем в (10.9) и получим новое уравнение для полной работы экстратока размыкания, или — начального запаса энергии магнитного поля:
. (10.10)
здесь v = s×l — объём соленоида (магнитного
энергия катушки с током пропорциональна квадрату вектора магнитной индукции.
разделив эту энергию на объём магнитного поля, получим среднюю плотность энергии:
[]. (10.11)
это выражение похоже на выражение плотности энергии электростатического поля:
.
обратите внимание: в сходных уравнениях, если e0 — в числителе, m0 — непременно в знаменателе.
зная плотность энергии в каждой точке магнитного поля, мы теперь легко найдём энергию, в любом объёме v поля.
локальная плотность энергии в заданной точке поля:
.
значит, dw = wdv и энергия в объёме v равна:
.
см рисунок
Объяснение: