Question

18. За каждую секунду через поперечное сечение проводника проходит 50 электронов. Вычислите (в амперах) силу тока, протекающего по проводнику
(e= 1,6-10-1°Kл)

Answer 1

$I=\frac{50*1,6*10^{-19}}{1}=8*10^{-18}$ Ампер.

Объяснение:

Электрический заряд, перенесённый в единицу времени служит основной количественной характеристикой тока, которая называется сила тока. Данную характеристику нам и требуется найти:

Сила тока в данном случае находится исходя из формулы: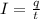 $I=\frac{q}{t}$ (1)

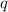Где $q$ - электрический заряд, 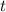$t$ - единица времени, в нашем случае секунда.

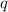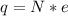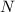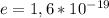Электрический заряд $q$ кратен элементарному заряду, то есть имеет вид: $q=N*e$, где $N$ - количество электронов, а $e$ - элементарный заряд, равный $e=1,6*10^{-19}$ Кл.

Поэтому подставляя формулу для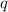 $q$ в формулу (1) получаем:

$I=\frac{N*e}{t}$

Все переменные нам известны, подставляем и считаем:

$I=\frac{50*1,6*10^{-19}}{1}=8*10^{-18}$ Ампер.