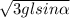Question

Небольшой шарик прикреплён с нити длиной l к гвоздю, вбитому в доску с гладкой
плоской поверхностью, наклонённой под углом α к горизонту
(см. рисунок). Вначале шарик удерживают на доске в точке A,
слабо натянув нить горизонтально вдоль доски. Какую минимальную скорость v0 надо сообщить шарику в точке A вдоль
доски перпендикулярно нити, чтобы шарик совершил полный
оборот, двигаясь по окружности?

ответы есть в Чешеве(это 1.124). Мне чень нужно именно понять как ее делать. Заранее !

Answer 1

Начальная скорость шарика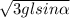  $\sqrt{3glsin\alpha }$

Объяснение:

Поскольку натяжение нити отсутствует то в верхней точке траектории шарика центробежная сила равна весу шарика.

На наклонной плоскости вес равен mgsin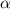$\alpha$

а центробежная сила m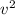$v^{2}$/L, тогда получаем первое уравнение

m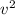$v^{2}$/L = mgsin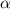$\alpha$ где скорость указана в верхней точке траектории.

Отсюда m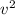$v^{2}$ = mgLsin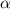$\alpha$ при сокращении получаем  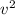$v^{2}$ = gLsin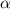$\alpha$

Используя закон сохранения энергии определяем энергию шарика в начальной точке и в верхней точке траектории. Они должны быть равны.

В начальной точке у шарика только кинетическая энергия, а в верхней кинетическая и потенциальная так как шарик поднялся на высоту Lsin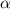$\alpha$

Пусть начальная скорость q тогда сначала энергия только кинетическая и равна m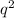$q^{2}$/2 а в верхней точке энергия состоит из кинетической m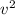$v^{2}$/2 и потенциальной mgLsin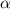$\alpha$ (скорость начальная и в верхней точке разные).

Получаем m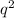$q^{2}$/2 = m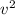$v^{2}$/2 +mgLsin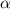$\alpha$ - это второе уравнение. Отсюда

m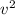$v^{2}$/2 = m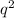$q^{2}$/2 - mgLsin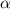$\alpha$ после сокращения и упрощения получаем

$v^{2}$ = $q^{2}$ - 2gLsin$\alpha$

Из первого и второго уравнения получаем:

gLsin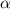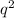$\alpha$ = $q^{2}$ - 2gLsin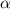$\alpha$

$q^{2}$ = 3gLsin$\alpha$

q = $\sqrt{3glsin\alpha }$