Рассчитать давление, производимое бетонной плиты, масса которой 780кг, а площадь опоры 4м2. Необходимо найти: а) силу давления б) давление

👇

Увидеть ответ

Ответ:

pv4419868

20.01.2020

m=780 кг;

S=2 м²;

Найти: p

Давление, производимое телом на опору, равно отношению веса тела к площади опоры:

\displaystyle p=\frac{P}{S}p=

Для ИСО вес тела равен силе тяжести:

\displaystyle P=mgP=mg

Откуда:

\displaystyle p=\frac{mg}{S}p=

Выполним расчет:

\displaystyle p=\frac{780*10}{2}=3900p=

780∗10

=3900 Па

ответ: 3900 Па.

4,6(62 оценок)

Открыть все ответы

Ответ:

andrejpyankoff

20.01.2020

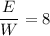
ответ: $\dfrac{E}{W} = 8$

Объяснение:

Запишем уравнение гармонических колебаний в общем виде:

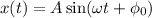
$x(t) = A \sin ( \omega t + \phi_{0})$

Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.

Отсюда 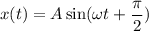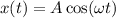$x(t) = A \sin ( \omega t +\dfrac{\pi }{2} )$ ⇒ $x(t) = A \cos ( \omega t)$ (1)

Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.

То-есть 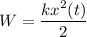$W=\dfrac{kx^{2}(t) }{2}$ , но согласно уравнению (1) получим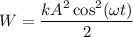 $W=\dfrac{kA^{2} \cos^{2} ( \omega t)}{2}\\$

Аналогично 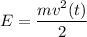$E = \dfrac{mv^{2}(t) }{2}$ , однако мы знаем, что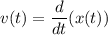 $v(t) =\dfrac{d}{dt} (x(t))$

Тогда 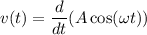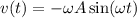$v(t) =\dfrac{d}{dt} ( A \cos ( \omega t))$ ⇒ $v(t) =-\omega A \sin( \omega t)$ , а это значит что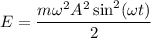 $E = \dfrac{m\omega^{2} A^{2} \sin^{2} ( \omega t)}{2}$

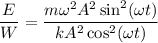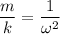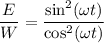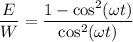Поэтому $\dfrac{E}{W} = \dfrac{m\omega^{2} A^{2} \sin^{2} ( \omega t)}{kA^{2} \cos^{2} ( \omega t)}\\}$ , так как $\dfrac{m}{k} = \dfrac{1}{\omega^{2} }$ , то $\dfrac{E}{W} = \dfrac{\sin^{2} ( \omega t)}{\cos^{2} ( \omega t)}\\}$ ⇒ $\dfrac{E}{W} = \dfrac{1 - \cos^{2} ( \omega t)}{\cos^{2} ( \omega t)}\\}$ (2)

Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1) 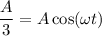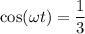$\dfrac{A}{3} = A \cos ( \omega t)$ ⇒ $\cos ( \omega t) = \dfrac{1}{3}$ , следовательно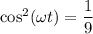 $\cos^{2} ( \omega t) = \dfrac{1}{9}$

Возвращаясь к уравнению (2) получим 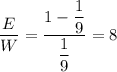$\dfrac{E}{W} = \dfrac{1 - \dfrac{1}{9} }{\dfrac{1}{9} }} = 8$

4,8(48 оценок)

Ответ:

tayatoadvel

20.01.2020

Закон сохранения механической энергии:

Ep + Ek = E

В начальный момент времени, когда мяч находится в высшей точке, его кинетическая энергия равна нулю, тогда уравнение закона:

Ep + Ek = Ep + 0 = Ep = E

В момент приземления потенциальная энергия мяча равна нулю, тогда:

Ep + Ek = 0 + Ek = Ek = E

Можно сделать вывод, что максимальная потенциальная (в начальный момент времени) и максимальная кинетическая (в момент приземления) равны друг другу и механической:

Ep max = Ek max = E

Тогда можем найти скорость мяча в момент приземления:

Ep max = Ek max

mgh max = mv² max/2 | : m

gh max = v² max/2

v² max = 2gh max => v max = √(2gh max) = √(2*10*5) = √100 = 10 м/с

Очевидно, что энергии будут равны тогда, когда каждая из них будет равна половине общей, а точкой, в которой это равенство произойдёт, будет точка, которая делит максимальную высоту пополам:

E/2 = Ep max/2 = Ep = Ek

mgh max/2 = mv²/2 | : m

gh max/2 = v²/2 | * 2

v² = gh max => v = √(gh max) = √(10*5) = √(25*2) = 5√2 = 5*1,41 = 7,05 = 7,1 м/с

ответ: 10 м/с, примерно 7,1 м/с.

4,7(57 оценок)

Это интересно:

Стиль-и-уход-за-собой

23.02.2022

Как ухаживать за вьющимися от природы волосами...

Образование-и-коммуникации

19.12.2022