Для твердых тел: увеличение объема происходит при их нагревании и носит название теплового расширения твердых тел:
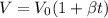
Где V₀ - начальный объем тела, t - температура нагрева,
β = (V₂-V₁)/V₁ - коэффициент объемного расширения
То есть для изменения объема твердого тела достаточно изменить его температуру.
Для газов: согласно уравнению состояния идеального газа:
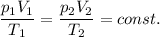
Где р - давление газа, V - объем газа, Т - температура газа.
Очевидно, что при постоянном давлении газа для изменения его объема также необходимо изменить его температуру.
1) Гармони́ческие колеба́ния — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.
Графики функций f(x) = sin(x) (красная линия) и g(x) = cos(x) (зелёная линия) в декартовой системе координат. По оси абсцисс отложены значения полной фазы.
2)Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
3) Собственная частота , также известная как собственная частота , - это частота, на которой система имеет тенденцию колебаться в отсутствие какой-либо движущей или демпфирующей силы. Схема движения системы, колеблющейся с собственной частотой, называется нормальным режимом (если все части системы движутся синусоидально с той же самой частотой). Если колебательная система приводится в движение внешней силой с частотой, на которой амплитуда ее движения является наибольшей (близкой к собственной частоте системы), эта частота называется резонансной частотой .
4) Негармонические колебания осуществляются в природе в системах, содержащих нелинейные элементы, которые преобразуют энергию источника в энергию колебаний.
Негармонические колебания, получающиеся в результате наложения двух одинаково направленных гармонических колебаний с близкими частотами ( to2 - ai K ( o), называются биениями.
Негармонические колебания выходят за рамки настоящей работы. Представляется, однако, целесообразным дать читателю хотя бы элементарные понятия и об этом вопросе.
5)Спектр колебаний (вибрации) — - совокупность соответствующих гармоническим составляющим значений величины, характеризующей колебания (вибрацию), в которой указанные значения располагаются в порядке возрастания частот гармонических составляющих.
6) Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения. Другой конец нити (стержня) обычно неподвижен. Период малых собственных колебаний маятника длины L, подвешенного в поле тяжести, равен
Математический маятник. Чёрный пунктир — положения равновесия,
θ
\theta — угол отклонения от вертикали в некоторый момент
T
0
=
2
π
L
g
и не зависит, в первом приближении, от амплитуды колебаний и массы маятника. Здесь g — ускорение свободного падения.
Математический маятник служит простейшей моделью физического тела, совершающего колебания: она не учитывает распределение массы. Однако реальный физический маятник при малых амплитудах колеблется так же, как математический с приведённой длиной.
« Пред.
§41. Применение законов динамики твердого тела
След. »
Как было установлено в предыдущих параграфах, движение твердого тела отвечает двум уравнениям [см. (35.5) и (38.5)]
(41.1)
(41.2)
Следовательно, движение тела определяется действующими на тело внешними силами fi и моментами этих сил Mi. Моменты сил можно брать относительно любой неподвижной или движущейся без ускорения оси (относительно той же оси берется и момент инерции I), Взяв моменты внешних сил относительно оси, движущейся с ускорением, мы, по существу, написали бы уравнение (41.2) в неинерциальной системе отсчета, В этом случае, кроме внешних сил, приложенных к телу, нужно учитывать также силы инерции и их моменты.
Точки приложения сил fi действующих на тело, можно переносить вдоль линий их действия, поскольку при этом ни сумма , ни моменты Mi не изменяются (при переноске силы вдоль линии ее действия плечо относительно любой точки не изменяется). Осуществляя такой перенос, можно несколько сил заменять одной силой, эквивалентной им в отношении воздействия, оказываемого на движение тела. Так, например, две силы f1 и f2, лежащие в одной плоскости (рис. 108), можно заменить эквивалентной им силой f, точку приложения которой можно также выбирать произвольно на направлении, вдоль которого она действует.
Объяснение:
Да, можем.
При нагрвании объём тела увеличивается т.к. расстояние между молекулами увеличивается.
При охлаждении объём тела уменьшается т.к. расстояние между молекулами уменьшается.