Объяснение:
Дано:
t₁ = 15 с
S₁ = 25 м
t₂ = 36 c
S₂ = 150 м
t₃ = 14 c
S₃ = 18 м
Vcp - ?
Средняя скорость:
Vcp = S / t
Vcp = (S₁ + S₂ + S₃ ) / (t₁ + t₂ +- t₃)
Vcp = (25 + 150 + 18) / (15 + 36 + 14) = 193 / 65 ≈ 3,0 м/с
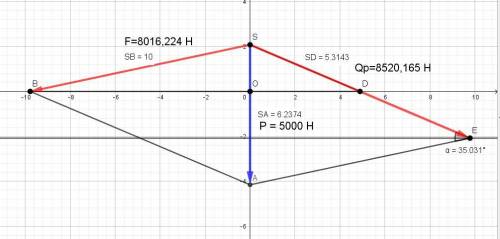
Заменим силу натяжения двух тросов на равнодействующую.
Здесь можно принять за аналогию треугольную пирамиду.
Проведём сечение через один из тросов с углом 12 градусов.
Равнодействующая будет равна двум апофемам.
Тангенс угла α наклона апофемы в 2 раза больше тангенса угла наклона троса.
tg α = 2*tg 12° = 2*0,212556562 = 0,425113123,
α = arc tg = 0,425113123 = 23,03098167 градуса.
Во вложении дана схема, на которой видно, то усилие в тросе соответствует гипотенузе прямоугольного треугольника, катетом которого есть третья часть вертикальной нагрузки.
P = (1/3)*500*10 = (5000/3) H.
F = (5000/3) / sin12° = 8016,224 H.
ответ: 145с; 662,5м
Объяснение: Путь трактора ДЭТ-250 за 2 минуты 25 секунд равен:
S1=2,5*145=362,5м
V1=9км/час=2,5м/с
t=2мин 25с=145с.
Ускорение второго трактора равно:
а=(V-Vo)/t=(5-0)/25=0,2м/с²
V2=18км/час=5м/с
Путь второго трактора за 25сек равен:
S2=Vo*t+at²/2=0,2*25²/2=62,5м
Расстояние между тракторами в момент начала равномерного движения равно:
S=S1-S2=362,5-62,5=300м
Скорость сближения тракторов равна:
V=V2-V1=5-2,5=2,5м/с
Время второго трактора, когда он догнал первый равно:
t=S/V=300/2,5=120с
Общее время второго трактора равно:
tобщ=120+25=145с
Путь второго трактора за 120с равен:
S=5*120=600м
Общий путь второго трактора когда он догнал первый равен:
Sобщ=600+62,5=662,5м
Объяснение:
Для того, чтобы определить среднюю скорость велосипедиста, необходимо использовать след. формулу:
υ ср =
υ ср = =
= ≈2.97
≈2.97
υ ср=2.97