Дано:
l=1 м.
n=1/3.
l₂=?
l₁=?
______
Длина всей цепочки:
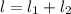
На первую часть цепочки (Которая свешивается со стола), действует сила тяжести Fт₁ равная m₁*g (масса той части цепочки, которая не лежит на столе). (Сила трения равна силе тяжести Fтр=Fт₁).
На вторую часть цепочки (которая не свешивается со стола) действует сила тяжести Fт₂ равная m₂*g (масса той часть цепочки, которая не свешивается). А так же сила реакции опоры N равная N=Fт₂.
Сила трения равна: Fтр=n*N; Fтр=Fт₁. (Из условия неподвижного блока - система меняет направление действия силы).
Запишем что мы получили:
Fт₁=n*N;
Fт₁=n*Fт₂.
m₁*g=n*m₂*g;
Теперь обратимся к массе, масса каждой части цепочки разная: m₁=p*V₁; m₂=p*V₂; (Плотность цепочки одинакова). Объемы распишем так: V₁=l₁*d; V₂=l₂*d; d - одинаков для всей цепочки, его сразу сокращаем.
l₁*g=n*l₂*g;
l₁=n*l₂;
Теперь возвратимся в самую первую формулу:
l=l₁+l₂; Сделаем замену l₁ как n*l₂
l=l₂*n+l₂;
l=l₂*(n+1);
Откуда l₂=l/(n+1);
l₂=1/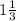
= 
метра. - Длина несвешивающейся части цепочки.
l₁=l-l₂=1-
=
метра.
ответ: l₁= метра - длина свешивающейся части цепочки.
начальная деформация h
массы брусков m1, m2
скорость первого бруска в момент когда отпускают второй
m1 v1^2 / 2 = k h^2 / 2
v1 = h корень (k / m1)
ведём отсчёт времени и координат брусков от момента и положений, когда отпускают второй
d^2 x1 / dt^2 = - k/m1 (x1-x2), d^2 x2 / dt^2 = - k/m2 (x2-x1)
dx1 / dt = v1 при t = 0, dx2 / dt = 0 при t = 0
вычитая из первого второе получим
d^2 (x1-x2) / dt^2 = (-k/m1 - k/m2) (x1-x2)
откуда ясно, что величина (x1-x2) будет испытывать гармонические колебания с частотой омега = корень (k/m1 + k/m2)
в начальный момент d(x1-x2) / dt = v1, x1-x2 = 0
при нулевой координате скорость максимальна
амплитуда равна максимальная скорость делить на частоту
A = v1 / омега = h корень (k / m1) / корень (k/m1 + k/m2) =
= h корень (1/m1) / корень (1/m1 + 1/m2) = h корень (m2/(m1+m2))
амплитуда величины x1-x2 это и есть максимальная деформация пружины
10 * корень (16/25) = 8