Реши задачу, пошагово выполняя указанные действия. Определи, на сколько градусов можно нагреть воду массой 618 кг при сжигании керосина массой 0,2 кг, если считать, что теплота, выделившаяся при полном сгорании керосина, целиком пошла на нагревание воды. Удельная теплоёмкость воды равна 4200 Дж/(кг·°С), удельная теплота сгорания керосина — 43 МДж/кг.
(ответ округли до десятых).

Шаг 1. Запиши формулу для нахождения количества теплоты, необходимого для нагревания вещества (воды) массой m на Δt°С, и заполни пропуски в пояснении к данной формуле: Qнагр=
⋅
в⋅Δ
,,

где

=
Дж/(кг·°С) — удельная теплоёмкость нагреваемого вещества (воды);

в =
кг — масса нагреваемого вещества (воды);

Δ
— изменение температуры вещества (воды) в результате нагревания.

Шаг 2. Запиши формулу для нахождения количества теплоты, которое выделяется при полном сгорании топлива (керосина) массой m, и заполни пропуски в пояснении к данной формуле:

Qгор=
⋅
т, где

=
МДж/кг =
Дж/кг — удельная теплота сгорания топлива (керосина);

т =
кг — масса топлива (керосина).

Шаг 3. Согласно условию, теплота, выделившаяся при полном сгорании керосина, целиком пошла на нагревание воды. Значит, количество теплоты Qнагр равно количеству теплоты Qгор.

Приравняй выражения для Qнагр и Qгор и в получившееся равенство подставь значения переменных (см. условие задачи, шаг 1 и шаг 2):

⋅
в⋅Δ
=
⋅
т,.

Подставь числовые значения физических величин:

4200⋅618⋅Δ
=
⋅106⋅
..

Шаг 4. Выполнив необходимые вычисления, реши получившееся линейное уравнение с точностью до десятых:

Δt =
°С.

👇

Открыть все ответы

Ответ:

lizagolovashko

27.12.2020

Для всех трех задач вспомним, что радиус-вектор представляет собой гипотенузу прямоугольного треугольника, а его проекции на оси координат -- катеты этот треугольника.

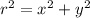
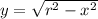
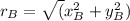
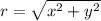
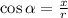
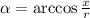
1) Известна гипотенуза и один из катетов, другой катет ищем по теореме Пифагора:

r^2 = x^2 + y^2

$y = \sqrt{r^2 - x^2}$

y = sqrt(5²-2,5²) м = 4,33 м

2) Известна гипотенуза и один из углов треугольника. Следовательно,

xA = rA * cos α = 5 м * cos 60° = 5 м * 1/2 = 2,5 м
yA = rA * sin α = 5 м * sin 60° = 5 м * sqrt(3) / 2 = 4,33 м

Складываем проекции вектора с проекциями радиус-вектора B относительно A:

xB = xA + xAB = 2,5 м + 1,83 м = 4,33 м
yB = yA + yAB = 4,33 м + 0 = 4,33 м

Радиус-вектор вычисляем через теорему Пифагора:

$r_B = \sqrt(x_B^2 + y_B^2)$

rB = sqrt(4,33² + 4,33²) м = sqrt(150/4) = 5/2 * sqrt(6) = 6,12 м

Поскольку xB = yB, то угол между вектором rB и осью Ox составляет 45°.

3) Известны оба катета треугольника, гипотенузу находим по теореме Пифагора:

$r = \sqrt{x^2 + y^2}$

r = sqrt(3² + 5,2²) м = 6 м

Чтобы вычислить угол с осью Ox, используем либо арксинус, либо арккосинус. В данном случае удобнее использовать арккосинус:

$\cos \alpha = \frac{x}{r}$

$\alpha = \arccos \frac{x}{r}$

α = arccos 3/6 = arccos 1/2 = 60°.

4,4(100 оценок)

Ответ: