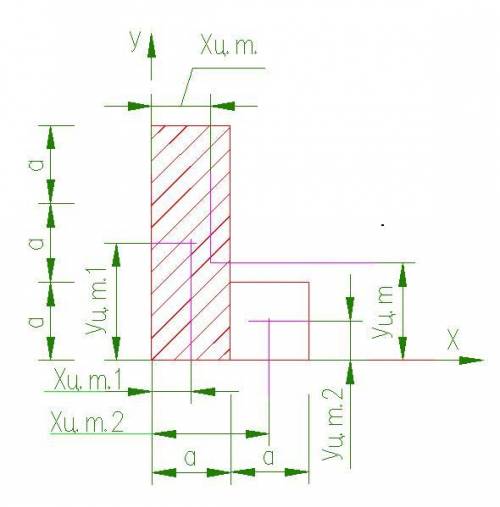
Объяснение:
Пластина делится на две прямоугольные части.
У прямоугольника центр тяжести в середине.
У первой - заштрихованной пластины площадь 3a^2
А расстояния от координатных осей до центра тяжести:
Хцт1=0,5а
Уцт1=1,5а
У второй пластины площадь a^2
расстояния от координатных осей до центра тяжести:
Хцт2=1,5а
Уцт1=0,5а
Центр тяжести можно найти если просуммировать площади умноженные на расстояние до центра тяжести каждой простой фигуры, а потом эту сумму поделить на общую площадь.
Общая площадь фигуры 4а^2
Остается посчитать
Хц.т.=(3a^2*0,5а+a^2*1,5а)/4а^2=3а^3/4а^2=3а/4=0,75а
Уц.т.=(3a^2*1,5а+a^2*0,5а)/4а^2=3а^3/4а^2=5а/4=1,25а
Картинка приложена
При смачивании, например водой стеклянного капилляра (краевой угол смачивания θ<90°) образуется вогнутый мениск, жидкость в капилляре поднимается. Это явление называется капиллярным поднятием жидкости. Жидкость поднимается тем выше, чем меньше радиус капилляра. Поверхность жидкости имеет отрицательную кривизну, поэтому дополнительное давление Лапласа стремится растянуть жидкость (давление направлено к центру кривизны) и поднимает ее в капилляре.
При несмачивании, например ртутью стеклянного капилляра (θ>90°), образуется выпуклый мениск, уровень жидкости в капилляре опускается. Это явление называется капиллярной депрессией. Жидкость опускается тем ниже, чем меньше радиус капилляра. Кривизна поверхности жидкости будет положительной, дополнительное давление Лапласа направлено внутрь жидкости (жидкость будет сжиматься), в результате чего жидкость в капилляре опускается.
Высота поднятия (понижения) уровня жидкости в капилляре:
h = 2σcosθ/((ρ-ρ₀)gR), где σ - коэффициент поверхностного натяжения искривленной поверхности, разделяющей жидкую и газообразную фазы, R - радиус капилляра, θ - краевой угол смачивания, ρ - плотность жидкости, ρ₀ - плотность газа, п - ускорение свободного падения 9,81 м/с²
Это выражение носит название уравнения Жюрена