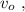

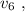
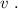
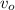 до
до  и от состояния
и от состояния  до
до  – одинаковы, а значит и изменение скорости одинаковое, поскольку движение равноускоренное:
– одинаковы, а значит и изменение скорости одинаковое, поскольку движение равноускоренное: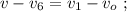 [1]
[1] до
до  – поезд проезжает расстояние вшестеро большее, чем от состояния
– поезд проезжает расстояние вшестеро большее, чем от состояния 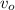 до
до 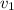 – а значит, средняя скорость
– а значит, средняя скорость  вшестеро больше средней скорости
вшестеро больше средней скорости 
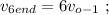
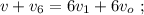
 [2]
[2]
 вагонов + локомотив.
вагонов + локомотив.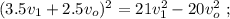
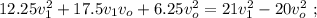
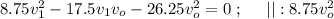
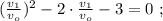
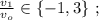
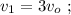
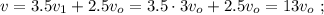

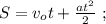
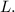
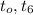 и
и 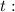
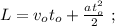 [1]
[1] [2]
[2]
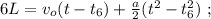
 то, используя [1]:
то, используя [1]:

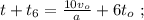
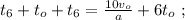
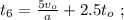
 [3]
[3]


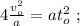
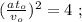
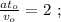

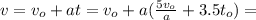
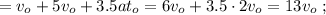

Будем измерять время от состояния
Пусть через время
Пусть состояния
Состояния
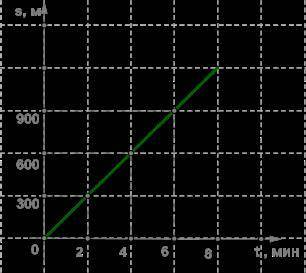
Через средние скрости, ясно, что:
Кроме того:
Складывая [1] и [2], получаем:
Учитывая [4], получаем:
Разделим последние уравнения:
За это время скорость дорастает от значения
При том же ускорении за первый интервал
Средняя скорость за время проезда локомотива:
Средняя скорость за время проезда всего поезда:
Перемножим [6] и [7] крест-накрест:
С учётом [5] имеем:
ОТВЕТ:
Например, при
при
при