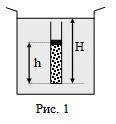
ответ: за 98 секунд
Объяснение:
Запишем «Дано»:
N = 1,5 кВт = 1500 Вт
Vв = 500 л =>
=> mв = 500 кг
h = 30 м
Чтобы поднять 500 кг воды на высоту 30 м, насос должен совершить работу, которую можно вычислить по формуле
А = F*S = m*g*S, где
F — сила, которую нужно приложить для поднятия воды, m — масса воды, g — ускорение свободного падения, S — перемещение воды (в данном случае оно равно высоте поднятия воды h).
!Вообще формула работы записывается как А = FS*cos a, где а — угол между направлениями F и S. Если эту формулу ещё не проходили, нужно сразу использовать формулу без cos a. Если проходили, нужно уточнить, что в данном случае F сонаправлено с S, a = 0°, cos a = 1, а значит, формула записывается как А = FS*1 = FS !
Работа, совершённая насосом, рассчитывается по формуле
А = N*t, где
N — мощность насоса,
t — время его работы.
Следовательно,
А = А
mgS = Nt, или
mgh = Nt
Выразим отсюда время:
t =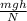 
Подставим значения:
t =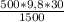 
= 98 (с)
Решение задачи предусматривет знание правила рычага (во сколько раз мы выигрываем в силе во столько раз мы проигрываем в расстоянии и - наоборот).
А также знание формулы по которой определяется такая физическая величина как РАБОТА.
А=FxH
То есть работа равна произведению силы F и расстояния Н , на которое переместилось тело ( нашем случае - поршень).
Если учитывать что малый и большой поршень совершили одинаковую работу , то можно составить уравнение
F1xH1=F2xH2 , где F1=500 Hьютонов -сила действующая на малый поршень
Н1= 0,15 М - перемещение малого поршня
F2=X - искомая сила , действующая на большой поршень
Н2= 0,05 М - перемещение большого поршня
500х0,15=Хх0,05
х=1500 Ньютонов