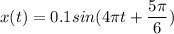по ф-ле Tомпсона
частота v=1/(2pi√(LC))
√C=1/(v2pi√L)
C=1/((v2pi)^2*L)
тогда
C1=1/((v1*2pi)^2*L)
C2=1/((v2*2pi)^2*L)
емкость сдвоенного конденсатора
С=С1+С2=1/((2pi)^2*L)*(1/v1^2+1/v2^2) (1)
частота с двойным конденсатором
v=1/(2pi√(LC))
v^2=1/((2pi)^2*LC))
подставим С из (1)
v^2=1/((2pi)^2*L)) * ((2pi)^2*L)*(1/v1^2+1/v2^2)
v^2= 1/v1^2+1/v2^2
из ф-лы видно , что квадрат частота равна сумме квадратов обратных величин частот при паралл.соедин.
подставим числа
v^2=1/20^2+1/30^2=(9+4)/3600=13/60^2
v=√13/60=0,06 кГц = 60 Гц
ответ: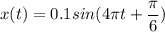
Объяснение:
Дано:
-----------------------------
Мы знаем что гармонические колебания материальной точки, можно описать с кинематических уравнений синуса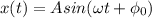 или косинуса
или косинуса 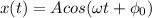
Где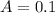 м - амплитуда колебаний МТ
м - амплитуда колебаний МТ
В том случае если мы используем уравнение косинуса
То в начальный момент времени, когда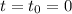 c
c
Отсюда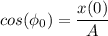
Соответственно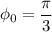 рад либо же
рад либо же 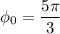 рад (это нам предстоит выяснить)
рад (это нам предстоит выяснить)
Однако, в том случае если мы используем уравнение синуса
То в начальный момент времени, когда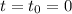 c
c
Отсюда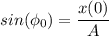
Соответственно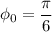 рад либо же
рад либо же 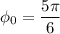 рад (это нам предстоит также выяснить)
рад (это нам предстоит также выяснить)
Таким образом получаем итоговые уравнения
1.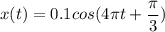
2.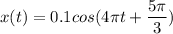
3.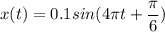
4.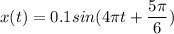
Теперь чтобы понять какие уравнения можно записать в итоговый ответ, для решения конкретно этой задачи, нам сказано в условии следующее "В момент времени t0=0 точка двигалась в положительном направлении оси Ox" это значит, что если определим скорость МТ для всех уравнений в начальный момент времени и в каких либо из уравнений начальная скорость будет меньше 0 м/с, это будет свидетельствовать о том что данные уравнения является неверными, ведь это будет противоречить условию указанному выше.
Для начала поверим уравнения косинуса
1.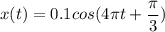
2.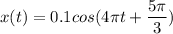
Теперь поверим уравнения синуса
3.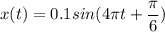
4.