4.У якому рядку наведено правильний порядок тактів роботи двигуна внутрішнього згоряння? ( ) а) Усмоктування, робочий хід, стиснення, випускання б) Випускання, стиснення, робочий хід, усмоктування в) Усмоктування, стиснення, робочий хід, випускання г) Усмоктування, стиснення, випускання, робочий хід

👇

Увидеть ответ

Ответ:

magamedgalaev9

30.08.2022

ответ В Усмоктування стиснення робочий хід випускання

4,8(98 оценок)

Открыть все ответы

Ответ:

564444

30.08.2022

Объяснение:

Виды добродетелей

Существует множество христианских добродетелей, и множество классификаций их.

Иногда добродетели разделяют на высшие и начальные.

Начальные: вера, покаяние, терпение, кротость, надежда, послушание, воздержание, милосердие, молитва, целомудрие и др.

Высшие: непрестанная молитва, смирение, любовь, бесстрастие, дар духовного рассуждения и др.

Преподобный Григорий Синаит разделяет добродетели на: деятельные, естественные и божественные

Деятельные суть дело благого произволения

Естественные происходят от сложения

Божественные – от благодати

Три главнейшие добродетели: воздержание, нестяжательность и смирение; пять за ними следующих: чистота, кротость, радость, мужество и самоуничижение, – и потом весь ряд прочих добродетелей.

Преподобный Ефрем Сирин делит добродетели на телесные, душевные и духовные

Телесные добродетели – это:

а) воздержание (пост),

б) молитвенное бдение (молитвенное правило и богослужение),

в) физический труд по самообеспечению и послушанию; и др. аскетические подвиги на благо ближних, требующие физических (телесных) усилий над собой.

Душевные: доброта, простота, почтительность, справедливость, великодушие, милосердие, щедрость, благородство, мужество.

Духовные: рассудительность, целомудрие, от которых рождаются вера, надежда, любовь, смирение, кротость, терпение, правдолюбие, свобода, сострадательность, богобоязненность, благодарность, умиление, благоговение.

Телесные добродетели должны служить душевным, душевные — духовным, а духовные — богопознанию. /Преп. Нил Синайский/

Часто выделяют добродетели естественные и сверхъестественные.

Естественные (свойственные человеческой природе (по естеству), в силу богообразности), такие как: человеческое благоразумие, милосердие, справедливость; человеческая благодарность, щедрость, снисходительность.

Сверхъестественные – Евангельские добродетели. «Какие расположения в сердце должно иметь христианину, указывают изречения Христа о блаженствах, именно: смирение, сокрушение, кротость, правдолюбие и истинолюбие, милостивость, чистосердечие, миролюбие и терпение» /свт. Феофан Затворник/

«Плод же духа: любовь, радость, мир, долготерпение, благость, милосердие, вера, кротость, воздержание. На таковых нет закона», т. е. они проистекают свыше, от Бога, по дару благодати, а не от следования только закону (Гал. 5:22-23).

Все христианские (евангельские) добродетели заключены в исполнении двух наиглавнейших заповедей – любви к Богу всем сердцем, разумением и силами души, и к ближнему как самому себе. (Иерархическая тримерия любви)

4,7(43 оценок)

Ответ:

Миша3456

30.08.2022

1. Структура электростатического поля
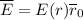
В силу симметрии задачи, электростатическое поле является центрально-симметричны. т.е. $\overline E = E(r) \overline r_0$
r₀ - единичный радиус-вектор от заряда к произвольной исследуемой точке пространства.
Задача и её решение инвариантна к повороту (как картинку "ни крути" вокруг заряда, условие задачи и её решение не изменится).

2. Поле при отсутствии шара
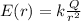Когда у нас есть только точечный заряд модуль напряженности электростатического поля $E(r) = k\frac{Q}{r^2}$ .

Потенциал электростатического поля связан с его напряженностью уравнением:
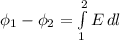
$\phi_1-\phi_2 = \int\limits^{2}_{1} {E} \, dl$
Интегрирование ведётся по произвольному пути между точками 1 и 2.

Отступление: если домножить уравнение на пробный заряд, то получим определение потенциальной энергии. Правый ингтеграл в этом случае будет работой, совершенной полем над пробным зарядом.

В нашем случае удобно интегрировать вдоль радиальных линий
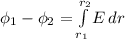
$\phi_1-\phi_2 = \int\limits^{r_2}_{r_1} {E} \, dr$

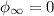
Замечание: Потенциал определяется всегда с точностью до аддитивной постоянной, поэтому во всех задачах всегда выбирается, так называемое, условие нормировки. В разных задачах оно выбирается по разному, но в задачах данного типа принято брать потенциал бесконечно удаленной точки равным нулю $\phi_\infty = 0$

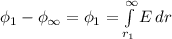
$\phi_1-\phi_\infty = \phi_1 = \int\limits^{\infty}_{r_1} {E} \, dr$

Подставим в эту формулу найденное поле:
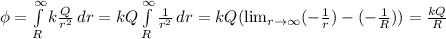
$\phi = \int\limits^{\infty}_{R} {k \frac{Q}{r^2} } \, dr = kQ\int\limits^{\infty}_{R} { \frac{1}{r^2} } \, dr = kQ ( \lim_{r \to \infty} (- \frac{1}{r}) - (- \frac{1}{R} )) = \frac{kQ}{R}$
Получили известный результат. Выразим из этого результата заряд Q.
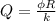
$Q= \frac{\phi R}{k}$

3. Поле при добавлении шара.
Для поиска величины напряженности воспользуемся теоремой Гаусса.
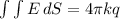
$\int {\int {E} } \, dS = 4\pi kq$
Поток вектора напряженности электростатического поля через любую замкнутую поверхность пропорционален величине свободного заряда, находящегося внутри этой поверхности.

Выберем в качестве такой поверхности сферу радиусом r. В силу структуры поля E(r) = const.
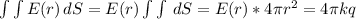
$\int {\int {E(r)} } \, dS = E(r)\int {\int {} } \, dS =E(r)*4\pi r^2 = 4\pi kq$
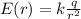
$E(r) = k \frac{q}{r^2}$

Теперь рассмотрим отдельные участки:
1) Участок 0 < r < 3R
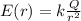
$E(r) = k \frac{Q}{r^2}$
2) Участок 3R<r<4R
E(r) = 0 - электростатического поля внутри идеальных проводников не существует. Если предположить противное, то начнётся движение зарядов и это уже не статика. :)
3) Участок r > 4R
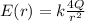
$E(r) = k \frac{4Q}{r^2}$
4Q - суммарный заряд внутри сферы радиусом r.

Аналогично рассчитаем потенциал.
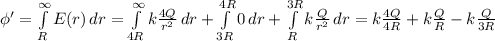
$\phi' = \int\limits^\infty_R {E(r)} \, dr = \int\limits^\infty_{4R} {k \frac{4Q}{r^2} } \, dr + \int\limits^{4R}_{3R} {0} } \, dr +\int\limits^{3R}_{R} {k \frac{Q}{r^2} } \, dr = k \frac{4Q}{4R} + k \frac{Q}{R} - k\frac{Q}{3R}$

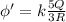
$\phi' = k \frac{5Q}{3R}$
Подставляем в это выражение найденное ранее Q и имеем:
$\phi' = \frac{5}{3}\phi = 500$

Что стоит отметить?
1) Потенциал функция непрерывная. Если знать, что подобные симметричные структуры создают поля аналогичные точечным зарядам, то задача решается в уме.
т.е. мы ищем потенциал на внешней границе шара как потенциал точечного заряда 4Q, на внутренней границе он такой же. Ищем разность потенциалов между внутренней границей и точкой A в поле точечного заряда Q. Складываем результаты.

2) Несмотря на то, что заряд 3Q на шаре поле внутри шара не создаёт, он увеличивает потенциал точек внутри полости, т.к. создаёт дополнительное поле вне шара. Потенциал - это работа по перемещению точечного заряда из бесконечности в данную точку. Больше поле вне шара - больше работа.

3) Разность потенциалов зависит только от локального поля (поля по в окрестности пути, соединяющего две точки). Сам потенциал зависит от структуры всего поля.

4,7(30 оценок)

Это интересно:

Финансы-и-бизнес

25.01.2020

Как открыть счет в швейцарском банке: необходимые шаги и требования...

Компьютеры-и-электроника

07.10.2020

Как переустановить Google Chrome: простой шаг за шагом гайд...

Кулинария-и-гостеприимство

18.06.2020

Замена бальзамическому уксусу - натуральные вкусовые альтернативы...

Компьютеры-и-электроника