Имеем: g = 1,6 м/c²; T = 4,9 c. Найти: L - ?
1. Формула периода математического маятника: 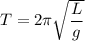 .
.
2. Выразим длину: 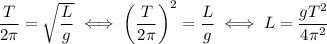 .
.
3. Численно получим: 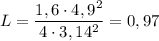 (м).
(м).
Дано: C = 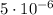 Ф; T = 0,001 c. Найти: L - ?
Ф; T = 0,001 c. Найти: L - ?
1. Формула Томсона: 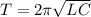 .
.
2. Индуктивность из (1): 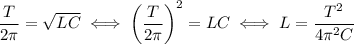 .
.
3. Численно получим: 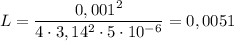 (Гн).
(Гн).
4. Перевод: 0,0051 Гн = 5,1 мГн.
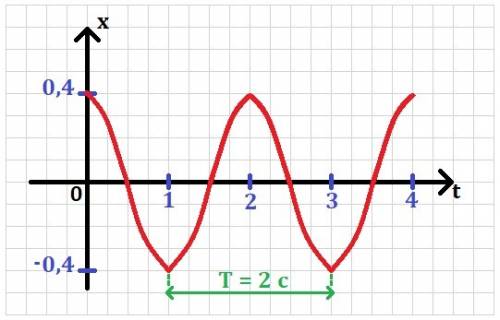
ответ: 5,1 мГн.======================Задача #3Имеем: x = 0,4cos(πt). Найти: A, T - ? Построить: x(t).
1. Уравнение гармонических колебаний в общем виде: 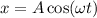 , отсюда амплитуда A = 0,4 м и циклическая частота ω = π рад/с.
, отсюда амплитуда A = 0,4 м и циклическая частота ω = π рад/с.
2. Формула циклической частоты: 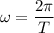 , значит период:
, значит период: 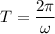 .
.
3. Численно: 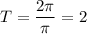 (c).
(c).
График зависимости x(t) смотри в приложении.
Тиск рідини на дно і стінки посудини
Тиск рідини на дно і стінки посудини
На кожну молекулу рідини, що знаходиться в полі тяжіння Землі, діє сила тяжіння. Під дією цих сил тяжіння кожен шар рідини тисне на розміщені під ним шари. За законом Паскаля цей тиск передається рідиною в усіх напрямах однаково. Отже, у рідинах існує тиск, зумовлений силою тяжіння показують, що рідина, яка знаходиться в посудині в стані спокою, тисне на дно і стінки посудини і на будь-яке тіло, занурене в цю рідину. Тиск, який чинить рідина на довільну поверхню тіл, розміщених у ній, називають гідростатичним.
Обчислимо значення цього тиску на глибині h у нестисливій рідині зі сталою густиною r. Вважатимемо, що прискорення земного тяжіння g не залежить від глибини. Виділимо всередині нерухомої рідини нерухомий елемент її об'єму DV у вигляді прямого циліндра висотою h з основами, що мають малу площу DS, паралельними вільній поверхні рідини (рис.2.4.8). Верхня основа циліндра знаходиться від поверхні рідини на глибині h1, а нижня - на глибині h2 (h2 >h1).
На виділений елемент об'єму рідини діють по вертикалі три сили: сили тиску F1 = p1 DS і F2 = p2 DS, де p1 і p2 - значення гідростатичного тиску на глибинах h1 і h2, та сила тяжіння F т = rgDV = r ghDS.
Виділений елемент об'єму рідини перебуває в спокої, тобто, , а отже, дорівнює нулю і алгебраїчна сума проекцій цих сил на вертикальну вісь, тобто p2DS – p1D S – rghDS, звідки
p2 – p1 = r gh. (2.4.5)
Нехай тепер верхня грань виділеного циліндричного об'єму рідини збігається з поверхнею рідини, тобто h1 = 0. Тоді h2 = h і p2 = pГ, де h - глибина занурення; pГ - гідростатичний тиск на цій глибині. Вважаючи, що на поверхні рідини гідростатичний p1 = 0 (тобто без урахування зовнішнього тиску на поверхню рідини) із (2.4.5) отримаємо формулу для гідростатичного тиску:
pГ = rgh. (2.4.6)
З урахуванням дії на вільну поверхню рідини тиску атмосфери p0 повний тиск на певній глибині h дорівнює:
p = p0 + rg h. (2.4.7)
Для газів формула (2.4.6) найчастіше незастосовна, бо їх густина досить швидко змінюється з висотою. Тому формулу (2.4.6) можна використовувати лише для порівняно тонких (метри і десятки метрів) шарів газів у полі тяжіння Землі.
Рівняння (2.4.7) дає змогу обчислити силу дії рідини на дно і стінки посудини. Часто враховують лише гідростатичний тиск pГ, бо повітря з усіх боків оточує посудини з рідинами, діючи на них.
Сила, з якою рідина діє на дно посудини, може бути, залежно від форми посудини, більшою або меншою від ваги налитої в посудину рідини. Це явище називають гідростатичним парадоксом.
Якщо в посудинах, форма яких різна, а площі дна S однакові, налити до однакового рівня рідину (рис. 2.4.9 - 2.4.11) густиною r, то сила, з якою рідина діє на дно, буде одноковою у всіх посудинах.
Дійсно, ця сила F = pS, де p - тиск на глибині h; S - площа дна. Але тиск рідини, що перебуває в спокої, не залежить від форми посудини, він залежить тільки від глибини h і густини рідини r:
pr = rgh.
Отже, у всіх посудинах рідина діє на дно з однаковою силою F = rghS, в той час, як вага рідини в різних посудинах різна.
"Гідростатичний парадокс" можна пояснити так. Сила , з якою рідина діє на стінку посудини, напрямлена перпендикулярно до стінки. За третім законом Ньютона стінка діє на рідину з такою ж за модулем і протилежною за напрямом силою . Розкладемо цю силу на дві складові - вертикальну і горизонтальну .
Як бачимо, у звуженій доверху посудині (рис. 2.4.9) сила напрямлена донизу, тому рідина тисне на дно із силою , більшою від ваги рідини . У посудині, розширеній доверху (рис. 2.4.10), навпаки, сила напрямлена вгору, тому рідина тисне на дно з силою , меншою за вагу рідини . У посудині з вертикальними стінками (рис. 2.4.11) = 0 і рідина діє на дно із силою, що дорівнює вазі рідини.
Складніше обчислити силу дії рідини на вертикальну стінку площею S = lh, де l - ширина стінки; h - товщина шару води, яка стикається зі стінкою. Із формули (2.4.6) випливає, що тиск на самий верх стінки дорівнює нулю, а біля її нижнього краю він дорівнює Pmax = rgh. З того, що залежність pг від глибини лінійна, випливає можливість записати середній тиск рідини на стінку у вигляді . Тому вся сила дії шару рідини завглибшки на вертикальну стінку
Гідростатичний тиск ураховують і для виведення умови рівноваги стовпів рідини у сполучених посудинах.
Сполученими називають такі посудини, які можуть вільно обмінюватись рідиною (наприклад, чайник і його носик), або такі, де тиск в одній посудині без змін передається в другу. Приклад останніх показано на рис. 2.4.12, на якому поршень В заважає змішуванню рідин, але передає взаємодію, бо зрівноважується тільки за однаковості тисків з обох боків. Якщо у лівому коліні посудини буде рідина густиною r1, а у правому - густиною r2, то за умови зрівноважування тисків на поршень з обох боків дістанемо:
Объяснение: