Объём полости ≈ 940 мм³
Объяснение:
Медный шарик в воздухе весит 5,34 Н, а в пресной воде 4,34 Н. Определить объем полости внутри шарика?
P₁ = 5.34 H
P₂ = 4.34 H
ρ₁ = 8960 кг/м³ - плотность меди
ρ₂ = 1000 кг/м³ - плотность воды
------------------------
ΔV - ? объём полости внутри шарика
------------------------
В воде вес шарика меньше, чем в воздухе, на величину архимедовой силы Fa = ρ₂ · g · V
Р₂ = P₁ - ρ₂ · g · V
Откуда объём шарика
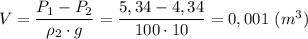
Вес шарика в воздухе
Р₁ = ρ₁ · g · (V - ΔV)
или
Р₁ = ρ₁ · g · V - ρ₁ · g · ΔV
Откуда объём полости

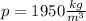
Введение и выражение величин:
Пусть плотность первой жидкости 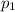 , второй жидкости
, второй жидкости 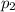 , а шара
, а шара 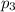 , тогда запишем общий объём шара
, тогда запишем общий объём шара 
Найдем объем шара находящийся над водой, для этого общий объем разделим на 4 (по условию), и получим 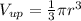 (1)
(1)
Повторим для нижней части шара, только умножим на 3/4, так как логично, что оставшаяся часть шара под разделом жидкостей, и получим 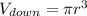 (2)
(2)
Чтобы найти массы этих частей шара, надо найденный объем умножить на плотность шара:
 (3)
(3)
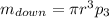 (4)
(4)
Работа с формулами и уравнением:
На шар действуют 2 силы: Архимеда и тяжести, так как шар неподвижен, то сила действующая на обе части "вниз", равна силе действующей на обе части "вверх", запишем общий вид:
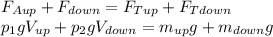
Подставим объем и массы из пунктов (1-4) и сократим на 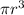 и на
и на  , в итоге останется:
, в итоге останется:
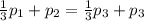
Подставим значения 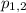 и решим уравнение:
и решим уравнение:
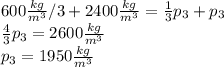
Получим те самые циферки из ответа
Дано:
F0- сила на поверхности земли
F- сила на высоте
F0=2F
Решение:
F0= GMз*m/R^2
F = GMз*m/(R+h)^2
F0/ F = 2 F/ F = GMз*m/R^2*(R+h)^2/ GMз*m ( здесь сокращаем все что можно и получаем)
2 = (R+h)^2/ R^2 | √
1.4R = R+h
h = 0.4R
ответ: h = 0.4R