До більшого плеча важеля прикріпили тіло масою 2 кг, а до меншого 800 г. Довжина малого плеча 20 см. Якою повинна бути довжина великого плеча, щоб важіль перебував у рівновазі?
Запишем уравнение гармонических колебаний в общем виде:
Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.
Отсюда ⇒ (1)
Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.
То-есть , но согласно уравнению (1) получим
Аналогично , однако мы знаем, что
Тогда ⇒ , а это значит что
Поэтому , так как , то ⇒ (2)
Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1) ⇒ , следовательно
1) в) 1360000 ДЖ. Здесь мы пользуемся формулой Q=Лямда *m Q=4*3,3*10(степени) При процесе крисстализации или отвердивании выделяется точно такое же количества теплоты как и при плавлении. 2) а) Только при больших температурах. Так как при больших температурах кинетическая энергия молекулы достигает такой скорости что приодолеть силу поверхностного натяжения других молекул. 3) а) У основания горы. Так как у основания горы атмосферное давление будет больше не жели на самой вершине 4) Здесь воспользуемся формулой Q=Lm Q= 2300*10(3степени) *3.5 =8050000 Дж
ответ: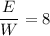
Объяснение:
Запишем уравнение гармонических колебаний в общем виде:
Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.
Отсюда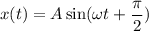 ⇒
⇒ 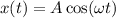 (1)
(1)
Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.
То-есть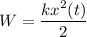 , но согласно уравнению (1) получим
, но согласно уравнению (1) получим 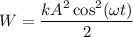
Аналогично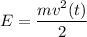 , однако мы знаем, что
, однако мы знаем, что 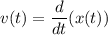
Тогда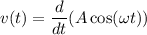 ⇒
⇒ 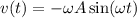 , а это значит что
, а это значит что 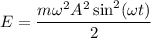
Поэтому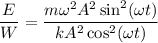 , так как
, так как 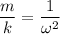 , то
, то 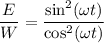 ⇒
⇒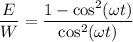 (2)
(2)
Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1)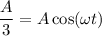 ⇒
⇒ 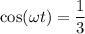 , следовательно
, следовательно 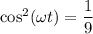
Возвращаясь к уравнению (2) получим