Более точное и полное объяснение этого явления дает так называемая теория Шмауса. Согласно этой теории состояние взвешенных в воздухе частичек аналогично состоянию вещества, находящегося в коллоидальном растворе. В таких растворах растворяемое вещество не расщепляется на молекулы, как в обычных, а остается взвешенным в растворителе в виде мельчайших частичек, представляющих собой скопление молекул.
Плотность растворенного вещества может оказаться больше плотности растворителя, но его частички совершенно равномерно распределяются во всем объеме растворителя и не осаждаются на дно, как это было бы в обычном растворе. Сила, поддерживающая эти частички, создается в результате беспорядочных ударов молекул растворителя, находящихся в так называемом молекулярном движении. Под действием этих ударов частички приходят в своеобразное зигзагообразное движение, известное под именем броуновского движения. Таким образом, источником силы, поддерживающей частички коллоидальных растворов, служит энергия молекулярного движения растворителя.
Источником силы, поддерживающей в атмосферном воздухе водяные капли, частички твердых тел и пр., служит существующее в нем так называемое конвективное или турбулентное движение. Это — беспорядочное движение отдельных частичек воздуха, вернее небольших его масс, в различных направлениях, независимое от общего потока воздуха.
Возникновение конвективного или турбулентного движения связано с механическим воздействием земной поверхности на движущиеся около нее воздушные массы.
Солнечные лучи неравномерно нагревают отдельные массы воздуха, выводят их из равновесия и заставляют подниматься вверх. Это, в свою очередь, вызывает горизонтальное движение воздуха и создает беспорядочное движение его отдельных частичек, перемешивая воздушные слои. Действие ударов отдельных частичек воздуха на пылинки поддерживает их в воздухе и каждая частичка адсорбирует к себе некоторое количество воздуха.
Получая от пылинки, при действии на нее солнечных лучей, значительное повышение температуры, адсорбированный в ней воздух расширяется и может создать небольшую подъемную силу, заставляющую пылинки медленно подниматься вверх или удерживаться на одном уровне.
Шмаус напоминает, что при растворении вещества в коллоидальном растворе частички его получают некоторый электрический заряд. Этот заряд зависит от природы растворителя и растворенного вещества. Поэтому, — рассуждает он, — несмотря на непрерывное беспорядочное движение частичек растворенного вещества, сцепления между ними не происходит, так как действует сила отталкивания одноименных зарядов.
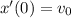 .
.
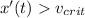 .
.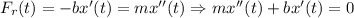
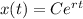 . Тогда дифференциальное уравнение имеет вид
. Тогда дифференциальное уравнение имеет вид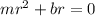
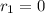
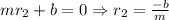
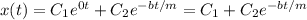
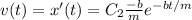
 ,
, 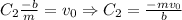 .
.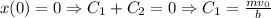
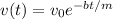
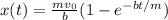
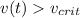 , то есть
, то есть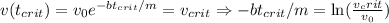
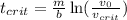
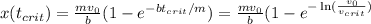
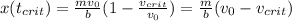
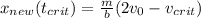
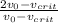 ,
,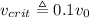 , это отношение равно
, это отношение равно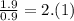 .
.
из формулы Томсона T= 2*п корень из L*C
найдем C=T^2/4*L*п^2=4,16 *10^-7=416 нФ