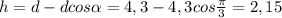 . Затем найдем скорость шара после соударения: согласно закону сохранения энергии
. Затем найдем скорость шара после соударения: согласно закону сохранения энергии 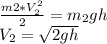 . Распишем закон сохранения импульса:
. Распишем закон сохранения импульса: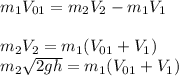 . Теперь закон сохранения энергии системы:
. Теперь закон сохранения энергии системы: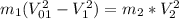 (это уравнение уже упрощенное). Дальше составляем систему из двух последних уравнений. Система выглядит во вложении(х - V_01, y-V_1). Решаем ее. x=363,93 y=357,38. Нам нужно y. Поэтому скорость пули после соударения равна 357,38 м/с. Все!
(это уравнение уже упрощенное). Дальше составляем систему из двух последних уравнений. Система выглядит во вложении(х - V_01, y-V_1). Решаем ее. x=363,93 y=357,38. Нам нужно y. Поэтому скорость пули после соударения равна 357,38 м/с. Все!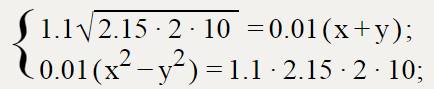
зависимость смещения x от времени t: X = A sin (ωt +φ)
А - амплитуда,
ω - угловая частота,
φ - начальная фаза.
Скорость - производная от смещения:
v = Aω cos (ωt +φ)
Ускорение - производная от скорости:
a = - Aω² sin (ωt +φ)
в этот момент φ=180 градусов, т.к. направления v и a противоположны
Тогда с учетом фазы
X = - A sinωt (1)
v = - A ω cos ωt (2)
a= Aω² sin ωt (3)
Разделим 1 на 3, получим X/a =- 1/ω²
ω = √a/x ω= √16 = 4
ω= 2π/T
тогда T = 2π/ω
T = π/2 cекунд
циклическая частота γ= 1/T = 2/π c^ -1
Амплитуду найдем разделив 1 на 2
X/v = 1/ω * tg(ωt)
ωt = arctg (Xω/v)
ωt = arctg 1
A = -X/sin ωt
A = - 10/√2