Шайбу толкнули вверх вдоль наклонной плоскости. В некоторой точке плоскости шайба побывала дважды: через 1 с и через 3 с от начала движения. Какую скорость сообщили шайбе, если известно, что вершина траектории находится на расстоянии 1 м от основания плоскости ?
Дано:
t₁ = 1 с ;
t₂ =3 с ;
x(t₁) = x(t₂) ;
Максимум X = X_м = 1 метр .
(скорость в этой (в верхней) точке равна нулю: V_м= 0)
- - - - - - -
|V₀| - ?
ответ: 1 м /с .
Объяснение: Допустим коэффициент трения скольжения постоянно. Шайба движется вверх вдоль наклонной плоскости равномерно замедленно, останавливается ( при x м =1 м ) , а потом равноускоренное движется вниз без начальной скорости ( опять вдоль наклонной плоскости ) .
Можно показать , что верно уравнение движения :
x(t) =|v₀|*t - |a|*t²/2. (главное)
* * * x(t) =v₀ₓ*t +aₓ*t²/2 , где v₀ₓ и aₓ проекции скорости и ускорения * * *
* единицы измерения используемых в задаче физических величин в системе СИ : [ x] = м , [v₀] = м/c , [a]= м/c² *
По условию задачи : x(t₁) =x(t₂) , т.е.
|v₀|*1 - |a|*1²/2 = |v₀|*3 - |a|*3²/2 . ⇔ |a| =|v₀|/2 (1)
С другой стороны |v₀|² =2*|a|*X_м (2)
* * * (м/c)² ≡ (м/c²)*м * * *
Следовательно : |v₀|² =2*(|v₀|/2)*X_м ⇔
|v₀|² = |v₀|*X_м || :|v₀| ≠ 0 ⇒ |v₀| = X_м
|v₀| = 1 (м/c) .
** * P.S. V(t)² = v₀² - 2*a*S ⇒ v₀²= 2*a*S ,если V(t) =0 * * *
Точка 2 минус 90 мВ
Точка 3 минус 40 мВ
Объяснение:
Задачу допустимо решать с правил Кирхгофа. Имеем три узла, значит токовых уравнений нужно 3-1=2, в цепи шесть ветвей, из них три источника тока, количество контурных уравнений 6-3-(3-1)=1. Запишем их
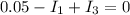
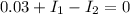
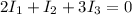
Решим систему методами линейной алгебры (на самом деле, если у вас есть другой любимый метод - можете решить им, главное получите правильные токи). Матрица коэффициентов
![A=\left[\begin{array}{ccc}-1&0&1\\1&-1&0\\2&1&3\end{array}\right]](/tpl/images/1358/3493/2e51b.png)
Ее определитель
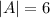- система не вырождена.
Найдем обратную матрицу (предварительно рассчитав алгебраические дополнения)
![A_1=\frac{1}{6}\left[\begin{array}{ccc}-3&1&1\\-3&-5&1\\3&1&1\end{array}\right] =\left[\begin{array}{ccc}-0.5&1/6&1/6\\-0.5&-5/6&1/6\\0.5&1/6&1/6\end{array}\right]](/tpl/images/1358/3493/eab9d.png)
Матрица токов
![\left[\begin{array}{c}I_1&I_2&I_3\end{array}\right] =\left[\begin{array}{ccc}-0.5&1/6&1/6\\-0.5&-5/6&1/6\\0.5&1/6&1/6\end{array}\right] \left[\begin{array}{c}-0.05&-0.03&0\end{array}\right] =\left[\begin{array}{c}0.02&0.05&-0.03\end{array}\right]](/tpl/images/1358/3493/34a22.png)
А
Значит токи в ветвях такие, как показаны на рисунке зеленым цветом.
Теперь легко найти потенциалы всех точек
Точка 2.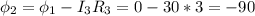 
мВ или же 
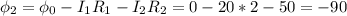мВ
Точка 3.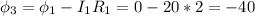 
мВ
Или 
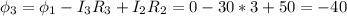мВ.
