Объяснение:
Дано:
R₁
R₂
m₁
m₂
A
___________
ω₁ - ?
1)
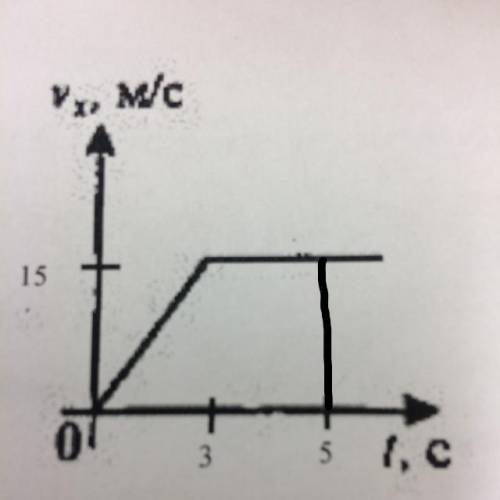
Поскольку колеса находятся в зацеплении, то линейная скорость точки А равна
V = V₁ = V₂
V₁ = ω₁·R₁ (1)
V₂ = ω₂·R₂ (2)
Приравняем (2) и (1)
ω₂·R₂ = ω₁·R₁
ω₂ = ω₁·R₁ / R₂
2)
Считаем зубчатые колеса тонкими обручами найдем их моменты инерции:
J₁ = m₁·R₁²
J₂ = m₂·R₂²
3)
Кинетические энергии колес:
T₁ = J₁·ω₁²/2
T₂ = J₂·ω₂²/2
Суммарная кинетическая энергия:
T = T₁+T₂ = J₁·ω₁²/2 + J₂·ω₂²/2
4)
По закону сохранения энергии:
T = A
J₁·ω₁²/2 + J₂·ω₂²/2 = A
J₁·ω₁² + J₂·ω₁²·R₁² / R₂² = 2·A
ω₁ = √ (2·A / ( J₁ + J₂·(R₁/R₂)²) )
где
J₁ = m₁·R₁²;
J₂ = m₂·R₂².
52,5 м
Объяснение:
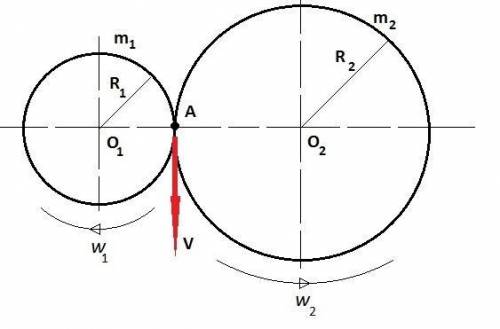
первые 3 с равноускоренно, так как уравнение скорости при равноускоренном движении : v=v0+at ( v0-начальная скорость, a-ускорение, t -время)
с 3 по 5 сек автомобиль движется равномерно,так как уравнение скорости при равномерном движении : v=s/t
перемещение(путь) находится как площадь фигуры под графиком скорости от времени v(t)
выбираем время 5 сек и смотрим на фигуру: это прямоугольная трапеция
формула площади трапеции:
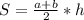
a,b-основания
h-высота
основания в данном случае равны 2(5-3) и 5(5-0)
высота равна 15
подставляем
s=7/2*15=3,5*15=52,5 м