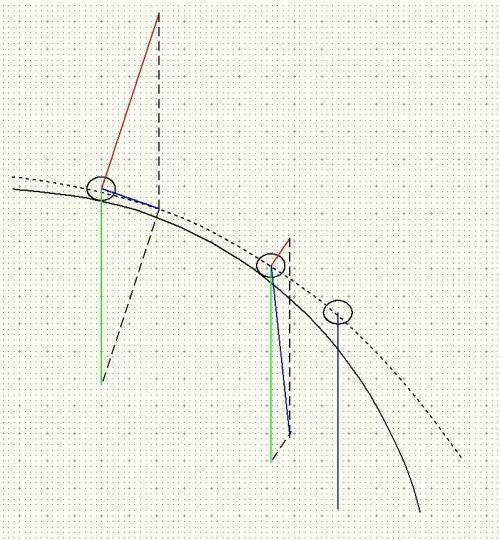
При движении по поверхности полусферы на тело действуют две силы – сила тяжести (зеленая) и сила реакции опоры (красная) . под действием равнодействующей этих сил (синяя) тело движется с ускорением, равным модуль равнодействующей делить на массу.
В момент отрыва от полусферы на тело действует только сила тяжести и не действует сила реакции опоры со стороны полусферы,
равнодействующая двух сил совпадает с силой тяжести
поэтому ускорение тела В момент отрыва от полусферы равно ускорению свободного падения.
Объяснение:
Дано:
Длина 1-ого участка пути: \bf S_1 = 10S
1
=10 км = \bf10\cdot10^310⋅10
3
м.
Время прохода 1-ого участка: \bf t_1 = 10t
1
=10 мин = \bf600600 с.
Длина 2-ого участка пути: \bf S_2 = 15,2S
2
=15,2 км = \bf15,2\cdot10^315,2⋅10
3
м.
Время прохода 2-ого участка: \bf t_1 = 20t
1
=20 мин = \bf12001200 с.
Найти нужно среднюю скорость: \bf < V > - ?<V>−?
Средняя скорость по определению - частное всего пути и всего времени: \boxed{\; < V > = \dfrac{S}{t}\;}
<V>=
t
S
, для данной задачи: < V > = \dfrac{S_1 + S_2}{t_1 + t_2}.<V>=
t
1
+t
2
S
1
+S
2
.
Численно получим:
< V > = \dfrac{10\cdot10^3 + 15,2\cdot10^3}{600 + 1200} = 14<V>=
600+1200
10⋅10
3
+15,2⋅10
3
=14 (м/с).
ответ: 14 м/с.
* Так как решение задачи мы начали с перевода заданных величин в СИ, ответ получился тоже в СИ - м/с.
Дано t=20 с V=1483 м/с H - ?
H = V*t/2=1483*20/2=
странное у вас дано время и водоем странный, очень глубокий
таких на земле нет