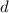 - прицельный параметр (его мы и будем искать потом).
- прицельный параметр (его мы и будем искать потом).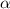 с горизонтом такой, что его синус
с горизонтом такой, что его синус 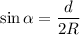 , где
, где 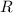 - радиус каждого из шаров.
- радиус каждого из шаров.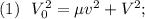
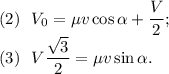
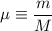 .)
.)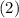 и
и 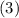 члены, содержащие выражения с фактором
члены, содержащие выражения с фактором 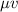 , возведем их в квадрат и сложим. Тогда около этого фактора после сложения окажется тригонометрическая единица. Так мы избавляемся от функции угла.
, возведем их в квадрат и сложим. Тогда около этого фактора после сложения окажется тригонометрическая единица. Так мы избавляемся от функции угла.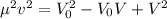
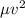 и подставим эту конструкцию в
и подставим эту конструкцию в 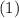 .
.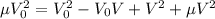 .
.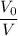 :
: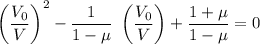 .
.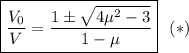 .
. и
и  . Опять выражаем из них выражения с фактором
. Опять выражаем из них выражения с фактором  , но в этот раз мы разделим одно на второе (косинус на синус, например). Получим:
, но в этот раз мы разделим одно на второе (косинус на синус, например). Получим: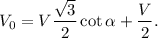
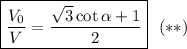 .
.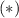 и
и  , находим одно тривиальное решение, отвечающее отсутствию удара вообще и одно нетривиальное, отвечающее равенству правых частей. Это равенство представляет из себя некое уравнение на угол. Теперь мы вспомним про самое первое уравнение, написанное в решении. Из него легко получить
, находим одно тривиальное решение, отвечающее отсутствию удара вообще и одно нетривиальное, отвечающее равенству правых частей. Это равенство представляет из себя некое уравнение на угол. Теперь мы вспомним про самое первое уравнение, написанное в решении. Из него легко получить 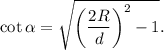
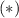 и
и  уравнение относительно прицельного параметра, получим окончательный ответ:
уравнение относительно прицельного параметра, получим окончательный ответ:![d=2R\left\{\dfrac13\left[1+\left(-1+2\dfrac{1\pm\sqrt{4\mu^2-3}}{1-\mu}\right)\right]^2\right\}^{-1/2}.](/tpl/images/0486/6836/a7d69.png)
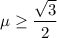 .
.
Вверху, т.к. тепло подымается вверх