Question

Длина недеформированной пружины 16 см. если к ней подвесить груз, длина пружины в положении равновесия станет равной 25 см. найти период малых вертикальных колебаний получившегося пружинного маятника

Answer 1

Дано: l1 = 16см ; l2 = 25см (l - длина)

Найти: T(период колебаний пружинного маятника) - ?

У нас дано две длины l1 - не деформированная, то есть не растянутая, а l2 уже растянутая. Найдём разность этих длин и получим l2-l1=25 - 16 = 9 (см) - это мы нашли удлинение пружины, то есть общее удлинение.

Чтоб рассчитать Период колебаний пружинного маятника, мы вспомним, что период колебаний бывает пружинного и нитяного маятников, нам из этого, нужен пружинный, следовательно находим формулу периода колебаний пружинного маятника: T= 2π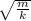$\sqrt{\frac{m}{k} }$. Нам неизвестна масса (m), за-то известно удлинение пружины.

Вспомним закон Гука: Fупр = k|x|, от сюда выразим удлинение k=F/|x| => От сюда мы можем заменить F = mg (Сила тяжести), следует k=mg/|x|, теперь вернёмся к формуле пружинного маятника T= 2π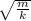$\sqrt{\frac{m}{k} }$, подставляем и получаем => T= 2π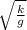$\sqrt{\frac{k}{g} }$ = 2*3,14*3/√10=5.961 округляем до целого и получаем 6(секунд).

ответ: T = 6 секунд