
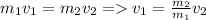
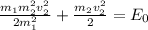
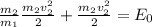
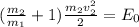
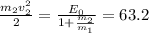 МэВ
МэВСреднюю скорость катера можно сосчитать по формуле:
\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}\]
Движение на обоих участках было равномерным, поэтому найти время \(t_1\) и \(t_2\) не составит труда.
\[\left\{ \begin{gathered}
{t_1} = \frac{{{S_1}}}{{{\upsilon _1}}} \hfill \\
{t_2} = \frac{{{S_2}}}{{{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
Так как участки равны по величине \(S_1=S_2=\frac{1}{2}S\), и скорость на первой участке больше скорости на втором в два раза \(\upsilon_1=2\upsilon_2\), то:
\[\left\{ \begin{gathered}
{t_1} = \frac{S}{{2{\upsilon _1}}} = \frac{S}{{4{\upsilon _2}}} \hfill \\
{t_2} = \frac{S}{{2{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
Подставим выражения для времен \(t_1\) и \(t_2\) в формулу средней скорости.
\[{\upsilon _{ср}} = \frac{S}{{\frac{S}{{4{\upsilon _2}}} + \frac{S}{{2{\upsilon _2 = \frac{S}{{\frac{{3S}}{{4{\upsilon _2 = \frac{{S \cdot 4{\upsilon _2}}}{{3S}} = \frac{{4{\upsilon _2}}}{3}\]
Значит необходимая нам скорость \(\upsilon_2\) определяется по такой формуле.
Дано:
V2=10 см^3=10^-5м^3
T1=10*С=283K
T2=100*С=373K
J=3 А/мм^2=3*10^6м^2
КПД=70 %.=0,7
t=1мин=60с
р=110*10^-8Oм*м
m1-?
КПД=Ап/Аз
Ап=Q=cm1(T2-T1), c=4200Дж/кг*К
Aз=I^2Rt, J=I/S, I=JS,V=SL, R=pL/S
Аз=(I/S)^2*pL/S=JpVt
КПД=cm1(T2-T1)/ JpVt
m1=КПДJ^2pVt/c(T2-T1)
m1=0,7*9*10^12*110*10^-8*10^5*60с/4200*90=11г