Используем формулу расчёта пройденного пути при равноускоренном движении: 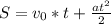
Отрезок t будет всегда равен единице, поскольку мы считаем пройденные путь за одну секунду.
Начальная скорость v0 будет равен для n-ой секунды (начиная с нуля) a*n, то есть с самого движения начальная скорость была a*0, после первой секунды мы уже разогнались до скорости a*1, после второй a*2
Тогда наша формула пройденного пути для n-ой секунды становится:
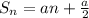
Можно составить пропорцию для S_n и S_n+1, то есть для n-ой секунды и следующей, так как мы знаем, что их отношение должно быть равно 3 и решить уравнение, найдя n
Но гораздо проще теперь просто подобрать:
S_0 = a/2 = 0.5 * a
S_1 = a + a/2 = 1.5 * a
S_2 = 2*a + a/2 = 2.5 * a
S_3 = 3*a + a/2 = 3.5 * a
Мы видим, что именно для S_1 (которая началась с первой секунды, то есть это вторая секунда) отношение с предыдущим 1.5*a / 0.5*a = 3, так что правильный ответ За вторую секунду
Дано:
t = 5 c
s = 50 м
s2(t2) - ?
Надо искать путь не за две секунды, а именно за вторую секунду.
s2(t2) - это путь тела за вторую секунду (двойка пишется как индекс величины).
Используем закономерность равноускоренного движения:
расстояния за равные промежутки времени соотносятся как ряд нечётных чисел, т.е.:
s1 : s2 : s3... = 1 : 3 : 5...
Таким образом, сравнивая s1 и s2, получаем:
s1/s2 = 1/3 => s2 = 3*s1
Расстояние s1 - это путь тела за первую секунду. Сначала выразим ускорение:
s = a*t²/2 => a = 2*s/t²
Теперь выразим s1:
s1 = a*t1²/2 = (2s/t²)*t1²/2 = s*t1²/t², следовательно, s2(t2) равно:
s2(t2) = 3*s1 = 3*s*t1²/t² = 3*50*1²/5² = 150/25 = 30/5 = 6 м
ответ: 6 м.
Дано:
t1=0’C
t2=49,9’C
m1=m
m2=m
с=4200Дж/кгС
L=330000Дж/кг
t-?
Q1=Lm/2- плавление льда массой m/2
Q2=cm∆t-нагрев воды , ∆t=t-t1
Q3=cm∆t2- остывание горячей воды ∆t2=t2-t
По закону сохранения энергии Q1+Q2=Q3
Lm/2+cm(t-t1)=cm(t2-t)
L/2+c(t-t1)= c(t2-t)
L/2+ct-ct1=ct2-ct
2ct= ct2+ ct1-L/2
t=(ct2+ ct1-L/2)/2c
t=[2c(t2+t1)-L]/4c
t=(2*4200*49,9-330000)/4*4200=5’C