1. Водитель автомобиля начал торможение, когда находился на расстоянии 200 м от заправочной станции и двигался к ней со скоростью 20 м/с. Какой должна быть сила торможения, чтобы автомобиль массой 1 т остановился около станции?
Дано:
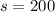 м
м
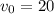 м/с
м/с
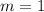 т
т 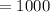 кг
кг
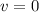
Найти: 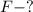
Решение. Направим горизонтальную ось 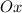 в сторону торможения автомобиля. Перейдем от проекций к модулям:
в сторону торможения автомобиля. Перейдем от проекций к модулям:
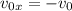
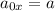

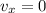
Тогда 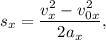 откуда
откуда 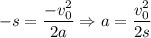
Применим второй закон Ньютона: 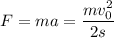
Определим значение искомой величины:
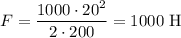
ответ: 1 кН
2. Сани движутся по горизонтальной дороге с начальной скоростью 5 м/с, коэффициент трения при этом равен 0,1. Найдите путь, который сани за 3 с.
Дано:
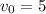 м/с
м/с
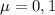
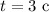
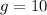 м/с²
м/с²
Найти: 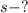
Решение. Направим горизонтальную ось 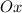 в сторону движения саней. Перейдем от проекций к модулям:
в сторону движения саней. Перейдем от проекций к модулям:
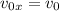
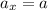
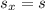
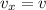
Тогда 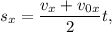 откуда
откуда 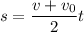
Найдем 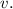
Применим второй закон Ньютона: 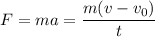
Сила трения: 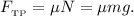
Поскольку 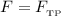 , то
, то
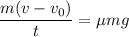
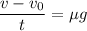
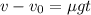

Таким образом, 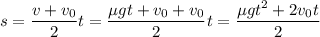
Определим значение искомой величины:
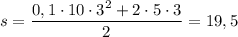 м
м
ответ: 19,5 м.
3. Автобус массой 10 т, двигаясь с места, развил на пути 50 м скорость 10 м/с. Найдите коэффициент трения, если сила тяги равна 14 кН.
Дано:
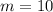 т
т 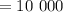 кг
кг
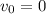
 м
м
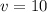 м/с
м/с
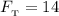 кН
кН 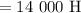
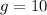 м/с²
м/с²
Найти: 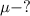
Решение. Направим горизонтальную ось 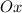 в сторону движения автобуса. Перейдем от проекций к модулям:
в сторону движения автобуса. Перейдем от проекций к модулям:
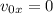
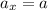
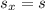
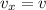
Тогда 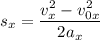 , откуда
, откуда 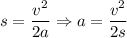
Применим второй закон Ньютона: 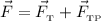
Перейдем от векторов к модулям:
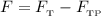
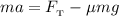
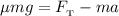
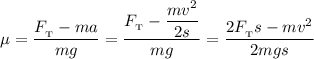
Определим значение искомой величины:
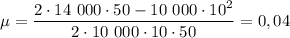
ответ: 0,04.
... НЕЗНАЮ и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть и в тех случаях может быть
V=0.02 м³
ρ = 250 кг/м³ – плотность пробки
ρ = 1000 кг/м³ – плотность воды
Рассчитаем массу воды, вытесненной пробковым кругом
m=ρ·V
m(воды)=1000·0.02
m(воды)=20 кг
Согласно закону Архимеда на круг действует сила равная весу воды, вытесненной кругом
Сам круг имеет вес:
m(круга)=250·0.02
m(круга)=5 кг
Находим массу, которую может удержать круг
m=20-5 m=15 кг
Круг может удержать массу 15 кг