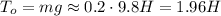Тепловоз мощностью 3000 квт имеет кпд двигателя 30%.определите,какую массу дизельного топлива с удельной теплотой сгорания 44,7 мдж/кг необходимо использовать для работы тепловоза на протяжении 1 часа.решение обязательно!

👇

Ответ:

Polina300696

22.03.2020

Q=m*q - сгорание топлива массы m приводит к выделению теплоты Q
W - полезная энергия
N - полезная мощность
W = N*t = Q*кпд / 100% = m*q*кпд / 100%
N*t = m*q*кпд / 100%
m = N*t / (q*кпд / 100%) = 3*10^6 * 3600 / (44,7*10^6 * 30 / 100) = 805,3691275 кг ~ 805,4 кг ~ 805 кг - это ответ

4,6(45 оценок)

Открыть все ответы

Ответ:

aluanakim

22.03.2020

Для начала отвлечёмся немного от конкретного вопроса и поставим такой мысленный эксперимент:

Допустим, мы сидим на высоком упругом куске поролона, теперь подложим ещё один точно такой же кусок поролона, что изменится? Понятно, что такое сиденье станет мягче, т.е. его жёсткость – снизится.

Вообще, верно такое положение: чем больше протяжённость одного и того же материала вдоль оси сжатия (растяжения) – тем меньше коэффициент жёсткости (упругости) такой пружинящей системы.

Проще говоря, рассматривая пружинки и резинки, можно сказать, что если из одного и того же материала изготовить одинаковые пружинки разной длины, то коэффициент жёсткости (упругости) будет больше у короткой и меньше у длинной пружинки, и отличаться коэффициенты жёсткости будут во столько же раз, во сколько отличаются их длины.

Теперь поговори о нашем резиновом 20-сантиметровом шнуре. Сила, действующая в первом опыте на нижний конец шнура – это вес подвешенного груза, который в состоянии покоя равен силе тяжести, действующей на груз. Т.е. эта сила $T_o = mg \approx 0.2 \cdot 9.8 H = 1.96 H$ . Коэффициент упругости такого резинового шнура можно легко найти, исходя из закона упругости Гука: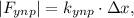

$| F_{ynp} | = k_{ynp} \cdot \Delta x ,$

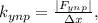
т.е. как: $k_{ynp} = \frac{ | F_{ynp} | }{ \Delta x } ,$

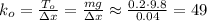или конкретно в нашем случае: $k_o = \frac{ T_o }{ \Delta x } = \frac{mg}{ \Delta x } \approx \frac{ 0.2 \cdot 9.8 }{ 0.04 } = 49$ Н/м .

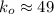Итак, жёсткость всего шнура $k_o \approx 49$ Н/м .

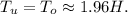Это воздействие в полной мере передаётся и точке закрепления шнура, и соответственно на верхнюю точку самого шнура действует сила $T_u = T_o \approx 1.96 H .$ Причём в любой точке шнура между его собственными частями действует такая же сила 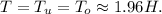$T = T_u = T_o \approx 1.96 H .$ А значит и в середине шнура действует точно такая же сила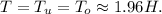 $T = T_u = T_o \approx 1.96 H .$

Середина шнура, находившаяся в нерастянутом состоянии на расстоянии 10 см от его концов, при равномерном растяжении всего шнура не перестаёт быть серединой, а значит, поскольку весь шнур становится 24 см длину, то середина оказывается в 12 см от концов шнура, т.е. перемещается вниз на 2 см, считая от верхней точки закрепления шнура. Отсюда можно вычислить коэффициент жёсткости именно верхней половины резинового шнура, которая при действии на неё силы Гука в 1.96 H

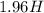удлиняется при растяжении на 2 см. И у нас получится: 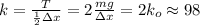$k = \frac{ T }{ \frac{1}{2} \Delta x } = 2 \frac{mg}{ \Delta x } = 2 k_o \approx 98$ Н/м . Откуда видно, что у половины шнура коэффициент упругости вдвое больше, чем у целого.

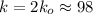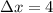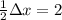Если бы мы подвесили груз просто к середине шнура, как показано в предпоследнем варианте, то шнур работал бы с коэффициентом упругости $k = 2 k_o \approx 98$ Н/м . А половина шнура, так же как и раньше, растягивалась бы на половину величины $\Delta x = 4$ см, заданной в условии, т.е. на $\frac{1}{2} \Delta x = 2$ см.

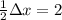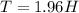А если же шнур не просто использовать на половину, а сложить и использовать обе его половины параллельно, как показано в последнем варианте, то каждая его часть при растягивании на $\frac{1}{2} \Delta x = 2$ см, действовала бы на груз с силой T = 1.96 H

, т.е. суммарная сила, действующая на груз вверх была бы вдвое больше необходимой для уравновешивания его массы, а значит, весь сложенный шнур немного поднимется, так что растяжение каждой его половинки сократится ещё вдвое, и общая сила натяжения станет равна силе тяжести груза.

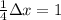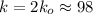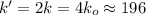Конечное растяжение сложенного шнура составит $\frac{1}{4} \Delta x = 1$ см. А его коэффициент упругости сложится из упругости одной и другой половинки сложенного шнура. А поскольку коэффициент упругости каждой половинки составляет $k = 2 k_o \approx 98$ Н/м, то коэффициент упругости всей такой системы будет $k' = 2k = 4 k_o \approx 196$ Н/м .

О т в е т :

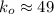$k_o \approx 49$ Н/м – коэффициент упругости исходного резинового шнура;

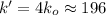$k' = 4k_o \approx 196$ Н/м – коэффициент упругости сложенного вдвое шнура;

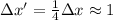$\Delta x' = \frac{1}{4} \Delta x \approx 1$ см

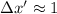*** важно понимать, что под $\Delta x' \approx 1$ см, здесь подразумевается длина, на которую удлиняется именно сложенный резиновый шнур, т.е. от

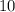см до

; если же гибким измерительным инструментом измерить полную длину сложенного резинного шнура, то она окажется равной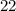

см, против исходных

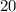см.

4,8(52 оценок)

Ответ:

LiveRiot

22.03.2020

, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра падают всё дальше и дальше от подножия скалы.

Теперь представьте, что вы забили в пушку столько пороха, что скорости ядра хватает, чтобы облететь вокруг земного шара. Если пренебречь сопротивлением воздуха, ядро, облетев вокруг Земли, вернется в исходную точку точно с той же скоростью, с какой оно изначально вылетело из пушки. Что будет дальше, понятно: ядро на этом не остановится и будет и продолжать наматывать круг за кругом вокруг планеты. Иными словами, мы получим искусственный спутник, обращающийся вокруг Земли по орбите, подобно естественному спутнику — Луне. Так мы поэтапно перешли от описания движения тела, падающего исключительно под воздействием «земной» гравитации (ньютоновского яблока), к описанию движения спутника (Луны) по орбите, не изменяя при этом природы гравитационного воздействия с «земной» на «небесную». Вот это-то прозрение и позволило Ньютону связать воедино считавшиеся до него различными по своей природе две силы гравитационного притяжения.

Остается последний вопрос: правду ли рассказывал на склоне своих дней Ньютон? Действительно ли всё произошло именно так? Никаких документальных свидетельств того, что Ньютон действительно занимался проблемой гравитации в тот период, к которому он сам относит свое открытие, сегодня нет, но документам свойственно теряться. С другой стороны, общеизвестно, что Ньютон был человеком малоприятным и крайне дотошным во всем, что касалось закрепления за ним приоритетов в науке, и это было бы очень в его характере — затемнить истину, если он вдруг почувствовал, что его научному приоритету хоть что-то угрожает. Датируя это открытие 1666-м годом в то

4,4(74 оценок)

Это интересно:

Компьютеры-и-электроника

20.12.2022

Как рассчитать наклон линии линейной регрессии в Excel: шаг за шагом...

Здоровье

20.08.2020

Как безболезненно сесть в позу лотоса: советы йогов и научное объяснение...

Образование-и-коммуникации

15.03.2022

Квантовая физика: с чего начать, чтобы понять ее?...

Дом-и-сад