1)
Дано:
pm = 3 A*м²
H = 300 A/м
R - ?
I - ?
1)
Пусть R - радиус кругового витка.
Площадь витка:
S = π*R²
Магнитный момент:
pm = I*S
2)
Связь магнитной индукции с напряженностью магнитного поля:
B = μ₀*H (1)
(μ₀ = 4π*10⁻⁷ Гн/м - магнитная постоянная)
Но магнитная индукция в центре витка:
B = μ₀*I / (2*R) (2)
Приравняем (1) и (2):
μ₀*H = μ₀*I / (2*R)
H = I / (2*R)
Домножим и разделим правую часть равенства на S:
H = I *S/ (2*R*S)
H = p / (2*R*S)
H = p / (2*R*π*R²)
H = p / (2*π*R³)
Отсюда радиус:
R = ∛ (p / (2*π*H) = ∛ (3 / (2*3,14*300) = 0,12 м или 12 см
3)
Сила тока:
I = 2*R*H = 2*0,12*300 = 72 A
Сила Архимеда находится по формуле 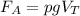 , мы видим, что зависимость силы идет от:
, мы видим, что зависимость силы идет от:
1) Плотности жидкости.
2) Объема погруженного в жидкость тела.
3) Ускорения свободного падения.
Масса тела находится по формуле 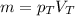 .
.
Поскольку по условию масса брусков одинакова, то из этого следует, что чем меньше плотность, тем больше объем тела.
Так как у алюминия плотность наименьшая, значит у него наибольший объем. А поскольку сила Архимеда зависит от объема, наибольшая сила выталкивания будет у алюминия.
ответ: на брусок алюминия.
По-хорошему, надо забить эту задачу в какой-нибудь мощный математический пакет и решить ее численно на компьютере (там интегрируются уравнения Лагранжа второго рода для каждого кусочка башни и земли). Более того, учесть влияние того, что башня закопана, тоже очень трудно.
Пренебрежем всем этим и решим задачу для наиболее простой модели. Пускай абсолютно твердая прямоугольная башенка размерами
Для того, чтобы башня упала, необходимо поставить ее на ребро-упор. А для этого нужно, чтобы момент прикладываемой силы был не меньше момента силы тяжести:
(здесь использовано определение момента силы - момент силы относительно точки есть векторное произведение радиуса вектора в эту точку на вектор силы). Если не знакомы с понятием векторного произведения, то просто скажу, что это произведение модулей векторов на синус угла между ними. Другими словами, модуль момента силы - это произведение модуля силы на расстояния до линии, вдоль которой она действует (плечо).
Поскольку все параметры башни нам известны, плечи можно отыскать без особого труда. Напишу сразу ответы для моментов в общем виде:
Подставим все это в условие опрокидывания и найдем ответ:
Напомню, это ответ для прямоугольной башни, мирно стоящей на столе в вакууме.