Дано: t1=20°C; t2=60°C; tc=38°C; V=80 л; m1 - ? m2 - ?
Тепло, отданное горячей водой = теплу, полученному холодной.
Q1 - Q2=0
Q=c*m*Δt
m1=ρV1=1000 кг/м³ * V1 дм³=1000 кг/м³ * 0,001*V1 м³=V1 кг
1 литр воды=1 дм³; его масса 1 кг.
с*m1*Δt1=c*m2Δt2 разделим на с
m(38 - 20)=(80 - m)(60 - 38)
18m=(80-m)*22
9m=(80-m)*11
9m=880 - 11m
20m=880
m=44 кг - холодная вода.
80 - 44=36 кг - горячая вода. Это ответ.
ИЛИ
с*m1*Δt1 - cm2*Δt2=0
ρ*V1*Δt1 - ρ*V2*Δt2=0
V1*Δt1=V2Δt2
V*(38-20)=(80-V)(60-38)
V=44 литра; т.к. 80 в литрах; m1=44 кг - хол. вода.
36 кг - горячая.
Рисунок к задаче в приложении.
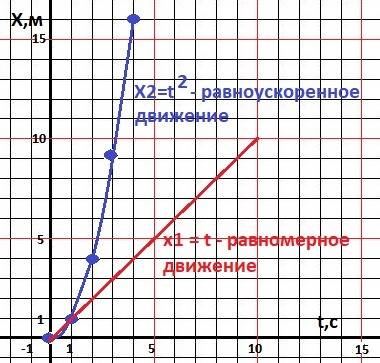
Равномерное движение описывается формулой
X(t) = Xo + V*t, где: Хо - начальное смещение, V - скорость движения.
График равномерного движения - квадратичная парабола. На рисунке - Xo = 0, V = 1,
При равномерном движении промежутки за равные интервалы времени будут одинаковыми - как и скорость, а их разность равна нулю - ускорение =0 - равномерное движение.
По графику функции можно сразу определить и Хо - сдвиг по оси Х и V - (коэффициент наклона прямой).
Равноускоренное движение описывается формулой
X(t) = Xo + Vo*t + a*t²/2, а графиком будет парабола. На рисунке: Хо=0, Vo=0, a = 2.
В этом случае разности перемещений за одинаковое времени будут составлять арифметическую прогрессию с разностью - d = 2 - ускорение движения.
Например, из рисунка находим значения перемещений:
Х = 1, 4, 9, 16, 25 - перемещения.
Находим первую разность и получим:
V = 3, 5, 7, 9 - скорости - равномерно увеличиваются.
Находим вторую разность и получим:
a = 2, 2, 2 - ускорение - постоянное - равноускоренное движение.
количество тепла одинаковое Q
вода Q=cm(T2-T1)=4200*0.440*(100-0)=184800 Дж
заготовка Q=c1m1*dT
dT=Q/(c1m1)= 184800 /(930*1)=198,70 = 199 град
ответ температура заготовки изменится на 199 град