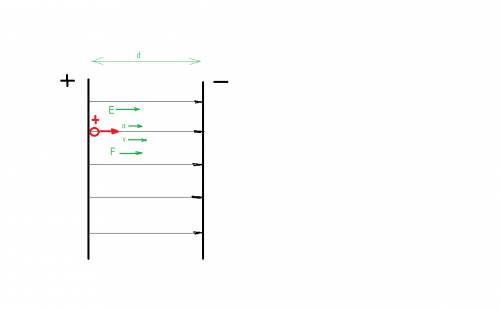
1)
дано
Vo= 0 м/с
t = 3c
q=2 нКл = 2*10^-9 Кл
m= 1 мг = 10^-6 кг
E =50 В/м
----------------
d - ?
решение
нужно определить расстояние по горизонтали, значит силу тяжести не учитывать
частица движется равноускоренно d = Vot +at^2/2 = at^2/2
ускорение a = 2d / t^2
сила по 2-му закону Ньютона F=ma
работа поля по перемещению частицы A= F*d=m*2d / t^2 *d = m*2*d^2 / t^2 (1)
разность потенциалов U=E*d
работа также по другой формуле A=q*U=q*E*d (2)
приравняем (1) (2)
m*2*d^2 / t^2 = q*E*d
d =q*E*t^2 / (2*m)
подставим значения из условия
d = 2*10^-9*50*3^2 / (2*10^-6)= 0.45 м = 45 см
ответ 0.45 м = 45 см
Условие задачи:
Парашютист, достигнув в затяжном прыжке скорости 55 м/с, раскрыл парашют, после чего за 2 с скорость уменьшилась до 5 м/с. Найти наибольшую силу натяжения строп парашюта, если масса парашютиста 80 кг.
Задача №2.1.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
υ0=55 м/с, t=2 с, υ=5 м/с, m=80 кг, T−?
Решение задачи:
Для того чтобы решить эту задачу, нужно схематично нарисовать парашютиста. На схеме следует изобразить силы, действующие на парашютиста: силу тяжести и силу натяжения строп. Так как человек уменьшил скорость падения, то его ускорение направленно вверх относительно Земли.
Запишем второй закон Ньютона в проекции на ось y.
T–mg=ma
Тогда сила натяжения строп равна:
T=mg+ma=m(g+a)(1)
Модуль ускорения легко определить по формуле определению:
a=|υ–υ0|t
Так как υ<υ0, то модуль в числителе раскрывается с противоположным знаком:
a=υ0–υt(2)
Подставим полученное выражение (2) в формулу (1).
T=m(g+υ0–υt)
Мы получили ответ к задаче в общем виде, теперь посчитаем ответ численно.
T=80(10+55–52)=2800Н
шарик летел бы время t
h=gt^2/2
t=корень(2*h/g)
при этом горизонтальное смещение составило бы S
S=t*v=корень(2*h/g)*v
так как шарик попал в щель, то путь S разбился на n частей, равных ширине щели L
n = S/L=корень(2*h/g)*v/L = корень(2*5/10)*7/2 = 3,5
значит шарик ударился о стенки 3 раза