Движение с горы - равноускоренное с ускорением а1. Найдем его:
S= a1t^2/2, a1 = (2S)/(t^2)
Тогда скорость в конце горы:
v = a1t = 2S/t = 8 м/с.
Движение по горизонтальному участку - равнозамедленное, с ускорением -а2
Уравнения кинематики:
v-a2t2 = 0 t2 = v/a2
s= vt2 - (a2t2^2)/2 Из этой системы получим: s = v^2/2a2.
Отсюда находим t2: t2 = 2s/v = 40/8 = 5 c.
Общее время движения: t + t2 = 15 c.
Средняя скорость по определению (весь путь поделить на все время):
Vср = (S+s)/(t+t2) = 60 / 15 = 4м/с.
ответ: 8 м/с; 15 с; 4 м/с.
Содержание: CИ:
t1= 10c 10 с
t2= 8 c 8 с
Найти: t0 - время опоздания.
Когда он выскочил на перрон, вагон, который он увидел, имел скорость
v0 = at0, (1)
где t0 - искомое время опоздания.
Рассмотрим, что происходило далее:
Пусть s -длина вагона.
Для промежутка времени t1 имеем след. ур-ия равноускоренного движения:
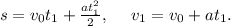 (2)
(2)
Здесь а - ускорение, а v1 - начальная скорость следующего проносящегося вагона (она же конечная скорость предыдущего вагона)
Для промежутка времени t2 уравнение перемещения вагона имеет вид:
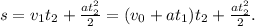 (3)
(3)
Теперь приравняв (2) и (3), получим выражение для v0:
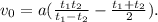
И наконец приравняв к (1), получим искомое время опоздания:
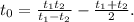
Теперь можем подставить t1 = 10, t2 = 8
t0 = 80/2 - 18/2 = 31 с.
ответ: опоздал на 31 с.
F2 = 5 H L2 = 0.195 м
Можно показать, что k = ΔF/ΔL:
L1 = L + F1/k
L2 = L + F2/k
Вычитая из первого равенства второе, получим:
L2 - L1 = F2/k - F2/k = (F2 - F1)/k
Откуда
k = (F2 - F1)/(L2 - L1)
Тогда
L = L1 - F1/k = L1 - F1(L2 - L1)/(F2 - F1) = 0.15 - 2(0.045)/3 = 0.12 м
Для проверки найдём нерастянутую пружину из второго уравнения:
L = L2 - F2/k = L2 - F2(L2 - L1)/(F2 - F1) = 0.195 - 5(0.045)/3 = 0.12 м
Как видно, всё сходится.