φо=0 рад
А= 5см = 0,05 м
Т=3 с
t=7 c
m=10 г= 0,01 кг
x, v, Ek -?
x=Acos(ωt+φо)
x=Acos(ωt)
ω=2π/T=2π/3
⇒ x=0,05cos(2πt/3) (рівняння коливань)
x=0,05cos(2*7π/3) = 0,05cos(14π/3) =
= 0,05cos((6+1)2π/3) = 0,05cos(6*2π/3 + 2π/3) =
= 0,05cos(4π + 2π/3) = 0,05cos(2π/3) = 0
Оскільки зміщення тіла в момент часу 7 с дорівнює нулю, то його швидкість максимальна (як і кінетична енергія), адже потенційна енергія мінімальна в точці рівноваги
v=Aω=0,05*2π/3≈0,1047 м/с =10,47 см/с
Ek = mv²/2 = 0,01*(0,1047)²/2 ≈ 5,5*10⁻⁵ Дж = 55 мкДж
5 с
Объяснение:
Запишем уравнение движения Фокса и Форда, приняв для последнего начальную координату за x₀₂ и скорость за v₂:
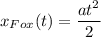
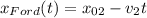
Тогда, расстояние между ними подчиняется закону:
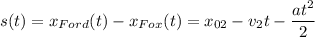
По условию, в некоторый момент времени τ это расстояние удовлетворяет условию:
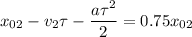
Скорости Фокса и Форда:
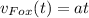
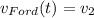
Их относительная скорость в момент времени τ:
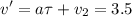 м/с
м/с
Подставляя все исходные данные в уравнения получим систему:
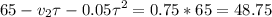
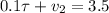
Выражаем скорость Форда из второго уравнения и подставляем ее в в первое:
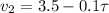
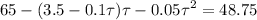
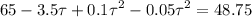
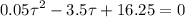
Решая полученное квадратное уравнение, находим два корня 65 и 5 секунд. Скорости Форда, соответствующие этим временам 3,5-0,1*5=3 м/с и 3,5-0,1*65=-3 м/с, значит нам подходит решение 5 секунд, так как для 65 секунд Форд идет не на встречу Фоксу, а убегает от него.
p=240 кг на м/c
По закону сохранения импульса импульс лодки после потери массы не изменился, изменилась лишь ее скорость
240=(m-80)*u
240=(240-80)*u
240=160u
u=1.5 м/c