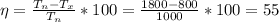 %
%
Объяснение:
А) напряжение на всей цепи равно 2В, но, тк резисторы 12(назовём это участок 1) и 34(а это участок 2)соединены параллельно, то напр. на участке 1 = напр. на участке 2 =1В
=> посчитаем силу тока на участке 2
I2=U2/R34
R34= R3+R4= 20+20=40(ом) т.к они соед. последовательно
I2=1/40=0,025А(сила тока на участке 2)
Резисторы соед. последовательно=> l'1=l'2=l2=0.025 A
Б) картина такая же как и в А
В) резисторы 1, 3 и 2 соед. параллельно, но 2 и 4 соед. последовательно.
На всем участке цепи напряжение 2 В.
Смотри , тк проводники соед. параллельно то на р1, р3 и р24(это резисторы 2+4 их напряжение складывается), напряжение равно 2В, значит на участке с резисторами р2 и р4 напряжение 2В, тк сила тока и сопротивление на них равно, то напряжение u2=u4=1В(uo=u2+u4), l2=l4=lo
=> I4= u3/R=1/20=0,05 A
Г) на всём участке цепи напр. 2В
Найдем общее сопротивление
р1 и р2 соед последовательно, значить Ro1=R1+R2=40
На участке с резисторами 3 и 4 также, тут Ro2
Rпараллели= ( Ro1*Ro2)/(Ro1+Ro2)= 40*40/50+40=2 Ом( эта блатная формула, можешь использовать школьную формулу Rп= (1/ Rо1)+(1/Rо2), итог будет такой же(если я не ошиблась в расчетах), просто эта формула, которой я пользуюсь, быстрее. Запомни ее и не усложняй себе жизнь)
Ro= Rп+ R3= 22 В
Найдем силу тока на всем участке
Io= Uo/Ro=2/22≈0,09 A
Параллельный участок и р3 соед последовательно, значит сила тока на параллели равна силе тока на р3 равна 0,09 А
Uпар= lR= 0,09*2≈0,18 В
I34=Uпар/R34≈0,0045 A
объяснение:
эффективный диаметр молекулы — минимальное расстояние, на которое сближаются центры двух молекул при столкновении.
при столкновении, молекулы сближаются до некоторого наименьшего расстояния, которое условно считается суммой радиусов взаимодействующих молекул. столкновение между одинаковыми молекулами может произойти только в том случае, если их центры сблизятся на расстояние, меньшее или равное диаметру d - — эффективному диаметру молекулы.
через эффективный диаметр молекулы можно выразить эффективное сечение молекулы — как круг радиусом d. столкновение между молекулами возможно только в том случае, когда центр молекулы окажется внутри круга, представляющего собой эффективное сечение молекулы.
с точки зрения теории межмолекулярных взаимодействий эффективный радиус, представляющий собой половину эффективного диаметра — расстояние от условного центра молекулы, отвечающее минимуму потенциальной энергии в поле этой молекулы.
для молекул, имеющих точечную симметрию, условный центр может быть определен как центр масс молекулы, для сложных молекул он определяется феноменологически.
в общем случае эффективный радиус — усредненная величина, т.к. в случае, когда молекула не является концентрически симметричной (одноатомная молекула), радиус является функцией от угла в системе, связанной с молекулой.
= (∫∫r(φ,θ)d×φ×d×θ)/2π²