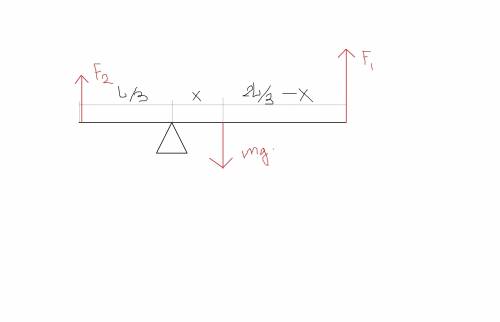
Для начала нужно нарисовать схему приложенных сил (см. рисунок).
Для равновесия этой системы необходимо, чтобы сумма моментов всех сил была равна 0. Запишем это условие математически, с учетом направления (со знаком "+" те силы, которые стараются повернуть рычаг по часовой стрелке, со знаком "-" - в обратную сторону):
F₂L/3 + mgx - 2F₁L/3 = 0
Легко видеть, что x = L/2 - L/3 = L/6
F₂L/3 + mgL/6 - 2F₁L/3 = 0
Разделим это уравнение на (L/6);
2F₂ + mg - 4F₁ = 0, отсюда:
m = 2(2F₁-F₂)/g = 2*(20-2)/10 =3.6 кг
Tumax=2πA
umax=2πΑ/Τ
А-амплитуда
Т-период
T=2π √L/g
L-длина нити
g-ускорение свободного падения=9,8~10 м/с^2
Т=2*3,14*√1,6/10
Τ=2,512 с^-1
Теперь амплитуда:
А=Lcosα=1,6*1/2=0,8
umax=2*3,14*0,8/2,512
umax=2 м/с
ответ:2
Амплитуду я нашел исходя из рассуждений,что амплитуда-это максимальное отклонение от положения равновесия.Максимальное отклонение от положения равновесия было при α=60°.Спроецировав я получил эту формулу,хотя не уверен в этом.